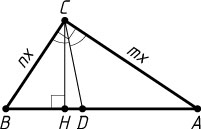
4628. В прямоугольном треугольнике ABC
проведена биссектриса CD
прямого угла C
. Известно, что AD=m
, BD=n
. Найдите высоту, опущенную из вершины C
.
Ответ. \frac{mn(m+n)}{m^{2}+n^{2}}
.
Решение. Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам, поэтому \frac{AC}{BC}=\frac{AD}{BD}=\frac{m}{n}
. Положим AC=mx
, BC=nx
. По теореме Пифагора
AB^{2}=AC^{2}+BC^{2},~(m+n)^{2}=m^{2}x^{2}+n^{2}x^{2},
откуда находим, что x^{2}=\frac{(m+n)^{2}}{m^{2}+n^{2}}
.
Пусть CH
— искомая высота. Выражая площадь треугольника ABC
двумя способами, получим, что
\frac{1}{2}AB\cdot CH=\frac{1}{2}BC\cdot AC,
следовательно,
CH=\frac{BC\cdot AC}{AB}=\frac{xn\cdot xm}{m+n}=x^{2}\cdot\frac{mn}{m+n}=\frac{(m+n)^{2}}{m^{2}+n^{2}}\cdot\frac{mn}{m+n}=\frac{mn(m+n)}{m^{2}+n^{2}}.
Источник: Вступительный экзамен в МФТИ. — 1969, билет 5, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 69-5-2, с. 133
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.18, с. 40
