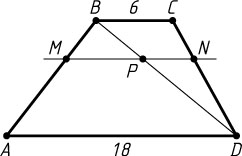
4658. Точка M
расположена на боковой стороне AB
трапеции ABCD
, причём AM:BM=2:1
. Прямая, проходящая через точку M
параллельно основаниям AD
и BC
, пересекает боковую сторону CD
в точке N
. Найдите MN
, если AD=18
, BC=6
.
Ответ. 10.
Решение. Проведём диагональ BD
. Пусть она пересекается с отрезком MN
в точке P
. По теореме о пропорциональных отрезках
\frac{BP}{PD}=\frac{CN}{ND}=\frac{BM}{AM}=\frac{1}{2}.
Треугольник BMP
подобен треугольнику BAD
с коэффициентом \frac{BM}{BA}=\frac{1}{3}
, а треугольник DNP
подобен треугольнику DCB
с коэффициентом \frac{DN}{DC}=\frac{2}{3}
, поэтому
MP=\frac{1}{3}AD=\frac{1}{3}\cdot18=6,~NP=\frac{2}{3}BC=\frac{2}{3}\cdot6=4.
Следовательно,
MN=MP+NP=6+4=10.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.2, с. 111
