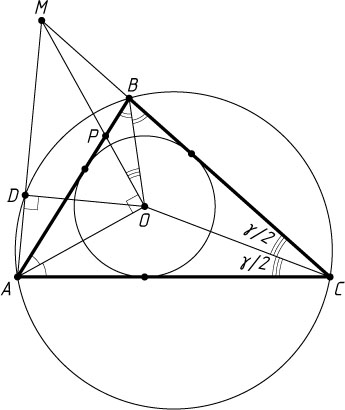
4670. Через центр O
вписанной в треугольник ABC
окружности проведена прямая, перпендикулярная прямой AO
и пересекающая прямую BC
в точке M
. Из точки O
на прямую AM
опущен перпендикуляр OD
. Докажите, что точки A
, B
, C
и D
лежат на одной окружности.
Указание. Треугольники MCO
и MOB
подобны.
Решение. Докажем сначала, что если O
— точка пересечения биссектрис треугольника ABC
, то \angle AOB=90^{\circ}+\frac{1}{2}\angle ACB
.
Действительно, сумма углов A
и C
треугольника ABC
равна 180^{\circ}-\angle C
, сумма их половин равна 90^{\circ}-\frac{1}{2}\angle C
, следовательно,
\angle AOB=180^{\circ}-\left(90^{\circ}-\frac{1}{2}\angle C\right)=90^{\circ}+\frac{1}{2}\angle C,
что и требовалось доказать.
Пусть прямая OM
пересекает сторону AB
данного треугольника ABC
в точке P
. Обозначим \angle ACB=\gamma
. По доказанному \angle AOB=90^{\circ}+\frac{\gamma}{2}
, поэтому
\angle BOM=\angle BOP=\angle AOB-\angle AOP=\left(90^{\circ}+\frac{\gamma}{2}\right)-90^{\circ}=\frac{\gamma}{2}=\angle BCO=\angle MCO,
значит, треугольник MCO
подобен треугольнику MOB
по двум углам (угол M
— общий), поэтому \frac{MC}{MO}=\frac{MO}{MB}
, откуда находим, что MO^{2}=MB\cdot MC
.
С другой стороны, отрезок OD
— высота прямоугольного треугольника AOM
, поэтому MO^{2}=MD\cdot MA
. Таким образом, MB\cdot MC=MD\cdot MA
. Следовательно, точки A
, B
, C
И D
лежат на одной окружности (см. задачу 114).
Автор: Филимонов В. П.
Источник: Московская математическая олимпиада. — 2008, LXXI, 11 класс
