4677. M
— точка пересечения диагоналей трапеции ABCD
. На основании BC
выбрана такая точка P
, что \angle APM=\angle DPM
. Докажите, что расстояние от точки C
до прямой AP
равно расстоянию от точки B
до прямой DP
.
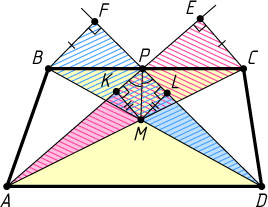
Решение. Пусть E
и F
— основания перпендикуляров, опущенных соответственно из точки C
на прямую AP
и из точки B
на прямую DP
, а K
и L
— основания перпендикуляров, опущенных из точки M
на прямые AP
и DP
соответственно. Тогда прямоугольный треугольник AKM
подобен треугольнику AEC
, а прямоугольный треугольник DLM
— треугольнику DFB
. Точка M
лежит на биссектрисе угла APD
, поэтому она равноудалена от сторон этого угла, т. е. MK=ML
. Из подобия треугольников AMD
и BMC
следует, что \frac{AM}{MC}=\frac{DM}{MB}
, поэтому \frac{AC}{AM}=\frac{DB}{DM}
, значит,
CE=KM\cdot\frac{AC}{AM}=ML\cdot\frac{DB}{DM}=BF,
что и требовалось доказать.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1996 г., второй тур, 9 класс
Источник: Московская математическая олимпиада. — 2008, LXXI, окружной этап, 9 класс
Источник: Берлов С. Л., Иванов С. В., Кохась К. П. Петербургские математические олимпиады. — СПб.—М.—Краснодар: Лань, 2003. — с. 69
