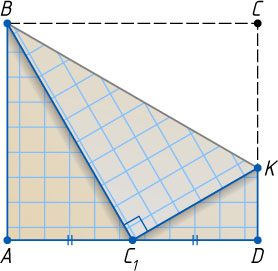
4678. Прямоугольный лист бумаги ABCD
согнули так, как показано на рисунке. Найдите отношение DK:AB
, если C_{1}
— середина AD
.
Ответ. 1:3
.
Решение. Из условия следует, что треугольники BC_{1}K
и BCK
равны, значит, BC_{1}=BC
, C_{1}K=CK
. В прямоугольном треугольнике ABC_{1}
катет AC_{1}
равен половине гипотенузы BC_{1}
, значит, \angle ABC_{1}=30^{\circ}
. Тогда
\angle AC_{1}B=60^{\circ},~\angle DC_{1}K=180^{\circ}-\angle AC_{1}B-\angle BC_{1}K=180^{\circ}-60^{\circ}-90^{\circ}=30^{\circ}.
В прямоугольном треугольнике KDC_{1}
катет, лежащий против угла в 30^{\circ}
равен половине гипотенузы, т. е.
DK=\frac{1}{2}KC_{1}=\frac{1}{2}CK.
Источник: Московская математическая олимпиада. — 2008, LXXI, окружной этап, 8 класс
