4679. Биссектриса, медиана и высота некоторого треугольника, проведённые из трёх разных вершин, пересекаются в одной точке и делят этот треугольник на шесть треугольников (см.рис.). Площади трёх закрашенных треугольников равны. Верно ли, что исходный треугольник равносторонний?
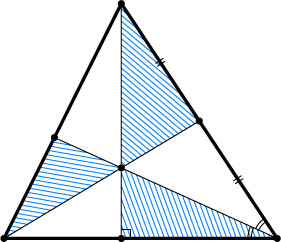
Ответ. Да.
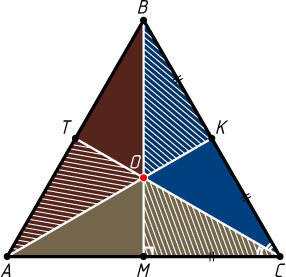
Решение. Пусть медиана AK
, высота BM
и биссектриса CT
треугольника ABC
пересекаются в точке O
. Треугольники AKB
и AKC
равновелики, так как у них равные основания (BK=CK
) и одна и та же высота (перпендикуляр, опущенный из точки A
на прямую BC
). Аналогично, равновелики треугольники треугольники BOK
и COK
, значит, равновелики треугольники COK
и COM
. По формуле для площади треугольника находим, что
S_{\triangle COK}=\frac{1}{2}CK\cdot CO\sin\angle OCK,~S_{\triangle COM}=\frac{1}{2}CK\cdot CM\sin\angle OCM,
а так как S_{\triangle COK}=S_{\triangle COM}
и \angle OCK=\angle OCM
, то CM=CK
, поэтому треугольники COK
и COM
равны по двум сторонам и углу между ними. Следовательно, \angle OKC=\angle OMC=90^{\circ}
, значит, медиана AK
треугольника ABC
является также его высотой, поэтому, треугольник ABC
— равнобедренный, AB=AC
.
Кроме того, из равенства CM=CK=\frac{1}{2}BC
следует, что в прямоугольном треугольнике BCM
катет CM
вдвое меньше гипотенузы BC
, значит, \angle BCM=60^{\circ}
. Таким образом, один из углов равнобедренного треугольника ABC
равен 60^{\circ}
. Следовательно, этот треугольник — равносторонний.
Источник: Московская математическая олимпиада. — 2008, LXXI, окружной этап, 10 класс

