4696. В окружности с центром O
проведены три равные хорды AB
, CD
и PQ
(см. рис.). Докажите, что угол MOK
равен половине угла BLD
.
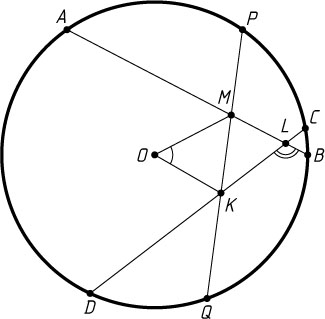
Указание. Равные хорды равноудалены от центра окружности, поэтому точка O
лежит на биссектриса угла AMQ
Решение. Равные хорды равноудалены от центра окружности, поэтому точка O
равноудалена от сторон угла AMQ
, значит, она лежит на биссектрисе этого угла. Аналогично, точка O
лежит на биссектрисе угла DKP
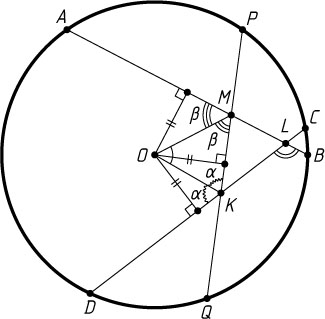
. Обозначим \angle OKM=\angle OKD=\alpha
, \angle OMK=\angle OMA=\beta
. Тогда
\angle MKL=180^{\circ}-2\alpha,~\angle KML=180^{\circ}-2\beta.
По теореме о внешнем угле треугольника
\angle BLD=\angle MKL+\angle KML=360^{\circ}-2\alpha-2\beta=2(180^{\circ}-\alpha-\beta)=2\angle MOK.
Следовательно, \angle MOK=\frac{1}{2}\angle BLD
, что и требовалось доказать.
Источник: Московская математическая олимпиада. — 2006, LXIX, окружной этап, 9 класс

