4713. Найдите площадь трапеции, у которой основания равны 10 и 26, а диагонали перпендикулярны боковым сторонам.
Ответ. 216.
Указание. Докажите, что данная трапеция — равнобедренная.
Решение. Пусть AD=26
, BC=10
— основания трапеции ABCD
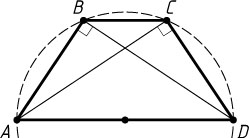
(рис. 1). Поскольку \angle ABD=\angle ACD=90^{\circ}
, то точки A
, B
, C
и D
лежат на окружности с диаметром AD
, т. е. около трапеции ABCD
можно описать окружность. Следовательно, ABCD
— равнобедренная трапеция.
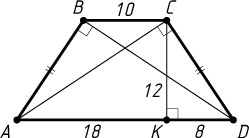
Пусть CK
— высота трапеции (рис. 2). Тогда
KD=\frac{AD-BC}{2}=8,~AK=\frac{AD+BC}{2}=18,
а так как CK
— высота прямоугольного треугольника ACD
, проведённая из вершины прямого угла, то CK=\sqrt{AK\cdot KD}=\sqrt{18\cdot8}=12
. Следовательно,
S_{ABCD}=\frac{AD+BC}{2}\cdot CK=18\cdot12=216.
Источник: Вступительный экзамен в МИФИ. — 1980
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 75, с. 190
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 13.41, с. 130
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 13.41.1, с. 140

