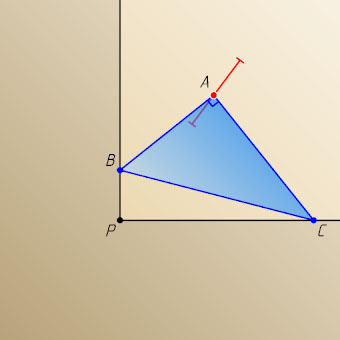
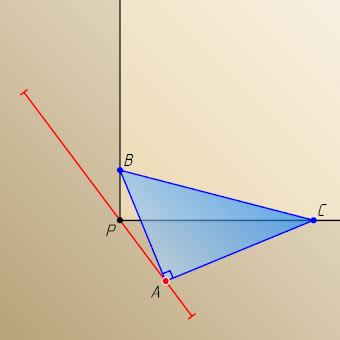
4721. Вершины B
и C
треугольника ABC
с прямым углом A
скользят по сторонам прямого угла с вершиной P
. Найдите геометрическое место вершин A
, если точки P
и A
лежат: а) по разные стороны от прямой BC
; б) по одну сторону от прямой BC
.
Ответ. Отрезок.
Указание. Точки P
и A
лежат на окружности с диаметром BC
.
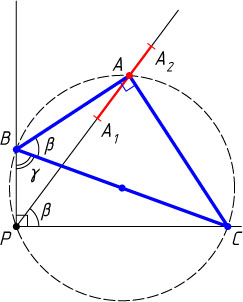
Решение. а) Пусть точки P
и A
лежат по разные стороны от прямой BC
(рис. 1). Обозначим \angle ABC=\beta
. Точки P
и A
лежат на окружности с диаметром BC
. Поэтому \angle APC=\angle ABC
, т. е. величина угла APC
постоянна. Следовательно, вершина A
перемещается по лучу. Если \angle ABC=\beta
, то этот луч образует со стороной PC
данного прямого угла угол \beta
.
Таким образом, точка A
лежит на луче l
с началом в точке P
и образующем угол \beta
со стороной данного прямого угла, по которой перемещается точка C
. Поскольку AP
— хорда окружности с диаметром BC
, то AP\leqslant BC
, причём, если катеты треугольника параллельны сторонам данного прямого угла, то AP=BC
.
Пусть \beta\geqslant45^{\circ}
. Обозначим \angle CBP=\gamma
. Поскольку 0\leqslant\gamma\leqslant90^{\circ}
, то
0\leqslant45^{\circ}-\frac{\gamma}{2}\leqslant45^{\circ}~\Rightarrow~\beta\geqslant45^{\circ}-\frac{\gamma}{2}~\Rightarrow~\angle ABP=\beta+\gamma\geqslant90^{\circ}-\beta=\angle BPA.
Значит, в треугольнике ABP
против большего угла ABP
лежит большая сторона AP
. Следовательно, AP\geqslant AB
. Причём, если точка B
совпадает с точкой P
, то AP=AB
.
Ясно, что при указанном в условии задачи перемещении треугольника ABC
точка A
опишет весь отрезок A_{1}A_{2}
(точки A_{1}
и A_{2}
таковы, что PA_{1}=AB
и PA_{2}=BC
), так как для каждого отрезка PA
такого, что PA_{1}\leqslant PA\leqslant BC
, можно найти соответствующий этому отрезку угол \gamma
и соответствующее положение треугольника ABC
(а может быть, и два положения).
Таким образом, длина отрезка, являющегося искомым геометрическим местом, равна BC-AB
, где AB
— наименьший катет треугольника ABC
.
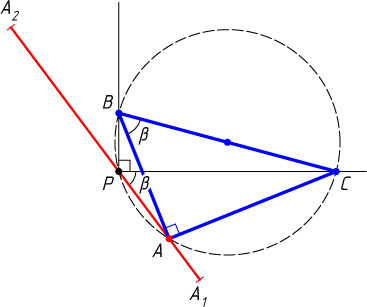
б) Если точки P
и A
лежат по одну сторону от прямой BC
(рис. 2), то с помощью аналогичных рассуждений получим, что искомое геометрическое место есть отрезок прямой, проходящей через точку P
и образующей со стороной PC
данного прямого угла, угол \beta
, причём длина этого отрезка равна сумме катетов треугольника ABC
.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 113, с. 105
Источник: Вступительный экзамен в МФТИ. — 1949, билет 16, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 49-16-3, с. 19
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 96
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 16, с. 205
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 27, с. 32
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.5, с. 31



