4726. Общая внутренняя касательная к окружностям с радиусами R
и r
пересекает их общие внешние касательные в точках A
и B
и касается одной из окружностей в точке C
. Докажите, что AC\cdot CB=Rr
.
Указание. Если O_{1}
и O_{2}
— центры окружностей, а C
и D
— точки касания окружностей с прямой AB
, то треугольники AO_{1}C
и O_{2}AD
подобны.
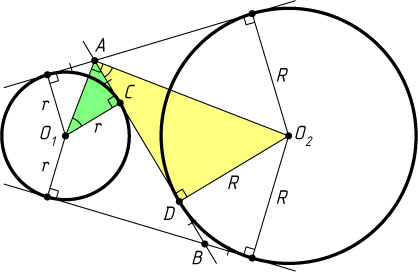
Решение. Пусть прямая AB
касается окружностей в точках C
и D
. Тогда BC=AD
.
Если O_{1}
и O_{2}
— центры окружностей, то \angle O_{1}AO_{2}=90^{\circ}
. Тогда прямоугольные треугольники AO_{1}C
и O_{2}AD
подобны. Поэтому \frac{O_{1}C}{AC}=\frac{AD}{DO_{2}}
. Следовательно,
AC\cdot CB=AC\cdot AD=O_{1}C\cdot DO_{2}=Rr.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.5, с. 59
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.5, с. 56
