4727. К двум окружностям различного радиуса проведены общие внешние касательные AB
и CD
. Докажите, что четырёхугольник ABCD
описанный тогда и только тогда, когда окружности касаются.
Указание. Четырёхугольник ABCD
описанный тогда и только тогда, когда биссектрисы его внутренних углов пересекаются в одной точке.
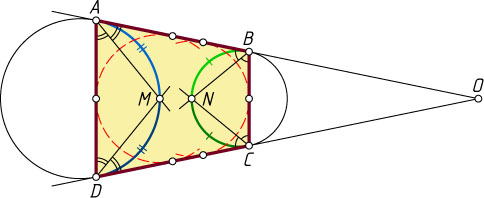
Решение. Пусть прямые AB
и CD
пересекаются в точке O
. Предположим, что точка B
лежит между O
и A
, а точка C
— между O
и D
. Тогда биссектрисы углов BAD
и CDA
пересекаются в точке M
— середине меньшей дуги AD
первой окружности, а биссектрисы углов ABC
и DCB
— в середине N
большей дуги BC
второй окружности.
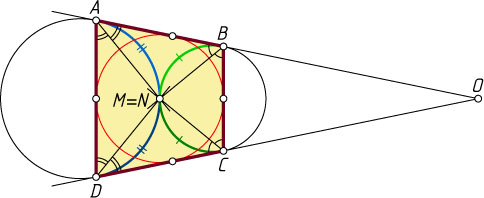
Четырёхугольник ABCD
описанный тогда и только тогда, когда точки M
и N
совпадают, т. е. когда данные окружности касаются.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.6, с. 59
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.6, с. 56

