4735. Две окружности пересекаются в точках A
и K
. Их центры расположены по разные стороны от прямой, содержащей отрезок AK
. Точки B
и C
лежат на разных окружностях. Прямая, содержащая отрезок AB
, касается одной окружности в точке A
. Прямая, содержащая отрезок AC
, касается другой окружности также в точке A
. Длина отрезка BK
равна 1, длина отрезка CK
равна 4, а тангенс угла CAB
равен \frac{1}{\sqrt{15}}
. Найдите площадь треугольника ABC
.
Ответ. \frac{5+\sqrt{15}}{4}
.
Указание. Треугольники ABK
и CAK
подобны.
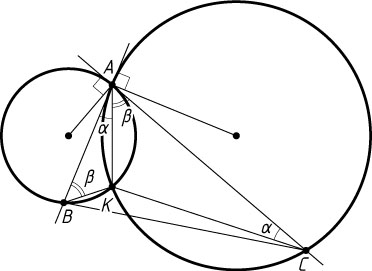
Решение. Обозначим \angle BAK=\alpha
, \angle CAK=\beta
. По теореме об угле между касательной и хордой
\angle ACK=\angle BAK=\alpha,~\angle ABK=\angle CAK=\beta.
Треугольники ABK
и CAK
подобны по двум углам. Поэтому \frac{BK}{AK}=\frac{AK}{KC}
. Отсюда находим, что AK=\sqrt{BK\cdot KC}=2
.
Поскольку
\tg\angle CAB=\tg(\alpha+\beta)=\frac{1}{\sqrt{15}}\gt0,
то угол CAB
— острый. Тогда
\cos(\alpha+\beta)=\frac{\sqrt{15}}{4},~\sin(\alpha+\beta)=\frac{1}{4}.
По теореме косинусов из треугольника AKB
находим, что
AB^{2}=AK^{2}+BK^{2}-2AK\cdot BK\cos\angle AKB=
=AK^{2}+BK^{2}-2AK\cdot BK\cos(180^{\circ}-\alpha-\beta)=
=4+1+2\cdot2\cdot1\cdot\frac{\sqrt{15}}{4}=5+\sqrt{15}.
Из подобия треугольников ABK
и CAK
следует, что AC=2AB
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin\angle BAC=AB^{2}\sin\angle BAC=\frac{5+\sqrt{15}}{4}.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1992, вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 195
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.13, с. 77
