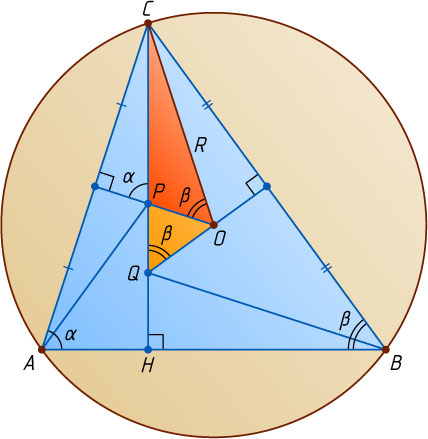
4739. Через центр окружности, описанной около треугольника ABC
, проведены прямые, перпендикулярные сторонам AC
и BC
. Эти прямые пересекают высоту CH
треугольника или её продолжение в точках P
и Q
. Известно, что CP=p
, CQ=q
. Найдите радиус окружности, описанной около треугольника ABC
.
Ответ. \sqrt{pq}
.
Указание. Рассмотрите равнобедренные треугольники APC
и BQC
и воспользуйтесь формулой a=2R\sin\alpha
.
Решение. Первый способ. Пусть R
— радиус окружности, описанной около треугольника ABC
, \angle BAC=\alpha
, \angle ABC=\beta
. Из равнобедренных треугольников APC
и BQC
находим, что
AC=2p\sin\alpha,~BC=2q\sin\beta.
Поскольку
AC=2R\sin\beta,~BC=2R\sin\alpha,
то
2p\sin\alpha=2R\sin\beta,~2q\sin\beta=2R\sin\alpha.
Перемножив почленно эти равенства, получим, что R^{2}=pq
.
Второй способ. Предположим, что ABC
— остроугольный треугольник. Тогда \angle COP=\angle ABC
и \angle OQP=\angle ABC
, значит, \angle COP=\angle OQP
.
Треугольники OQC
и POC
подобны по двум углам, следовательно, \frac{OC}{CP}=\frac{CQ}{OC}
, откуда R^{2}=CO^{2}=CP\cdot CQ=pq
.
Аналогично для тупоугольного треугольника.
Источник: Вступительный экзамен на физический факультет МГУ. — 1992, № 6, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.24, с. 113
