4743. В параллелограмме ABCD
угол BCD
равен 150^{\circ}
, а сторона AD
равна 8. Найдите радиус окружности, касающейся прямой CD
и проходящей через вершину A
, а также пересекающей сторону AD
на расстоянии 2 от точки D
.
Ответ. 2(5\pm2\sqrt{3})
.
Указание. Примените теорему косинусов. Задача имеет два решения.
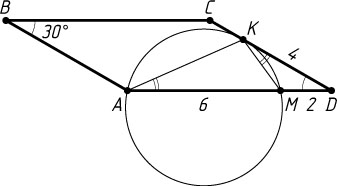
Решение. Пусть R
— искомый радиус, K
— точка касания указанной окружности с прямой CD
, M
— точка пересечения этой окружности со стороной AD
(DM=2)
. Тогда
DK=\sqrt{DM\cdot DA}=\sqrt{2\cdot8}=4.
Если точка K
лежит на луче DC
, то
MK^{2}=DM^{2}+DK^{2}-2DM\cdot DK\cos30^{\circ}=
=4+16-2\cdot2\cdot4\cdot\frac{\sqrt{3}}{2}=20-8\sqrt{3}=4(5-2\sqrt{3}).
Поскольку
\sin\angle MAK=\sin\angle DKM=\frac{DM\sin30^{\circ}}{MK}=\frac{1}{MK}
(теорема синусов), то
R=\frac{MK}{2\sin\angle MAK}=\frac{1}{2}MK^{2}=2(5-2\sqrt{3}).
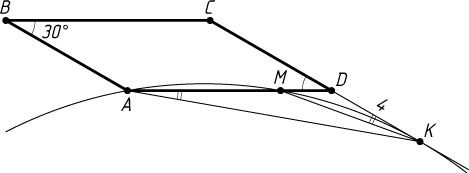
Если точка K
лежит на продолжении стороны DC
за точку D
, то
MK^{2}=DM^{2}+DK^{2}-2DM\cdot DK\cdot\cos150^{\circ}=4(5+2\sqrt{3}),
\sin\angle MAK=\sin\angle DKM=\frac{DM\sin150^{\circ}}{KM}=\frac{1}{KM}.
Следовательно,
R=\frac{MK}{2\sin\angle MAK}=\frac{1}{2}MK^{2}=2(5+2\sqrt{3}).
Источник: Вступительный экзамен на химический факультет МГУ. — 1992, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 601
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.29, с. 95

