4765. Окружности радиусов r
и R
касаются друг друга внутренним образом. Найдите сторону правильного треугольника, у которого одна вершина находится в точке касания данных окружностей, а две другие лежат на разных данных окружностях.
Ответ. \frac{rR\sqrt{3}}{\sqrt{r^{2}-rR+R^{2}}}
.
Указание. Примените теорему об угле между касательной и хордой и теорему косинусов.
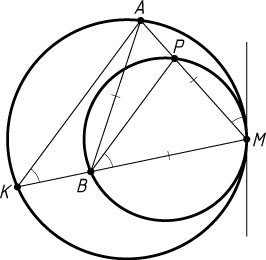
Решение. Первый способ. Пусть R\gt r
, AMB
— равносторонний треугольник, M
— точка касания окружностей, A
— точка на большей окружности, B
— на меньшей, P
— точка пересечения стороны MA
с меньшей окружностью, K
— точка пересечения продолжения стороны MB
с большей окружностью.
Углы MBP
и MKA
равны, так как оба они равны углу между прямой MA
(MP)
и общей касательной к окружностям, проведённой через точку M
. Следовательно, треугольники MBP
и MKA
подобны. Поскольку
BP=2r\sin\angle BMP=2r\sin60^{\circ}=r\sqrt{3},
AK=2R\sin\angle KMA=2R\sin60^{\circ}=R\sqrt{3},
то коэффициент подобия этих треугольников равен \frac{r}{R}
.
Обозначим MB=MA=AB=a
. Тогда
KM=\frac{aR}{r},~BK=a\left(\frac{R}{r}-1\right),
а так как \angle KBA=120^{\circ}
, то по теореме косинусов из треугольника ABK
находим, что
3R^{2}=\left(\frac{R}{r}-1\right)^{2}a^{2}+a^{2}+\left(\frac{R}{r}-1\right)a^{2}.
Отсюда следует, что a=\frac{rR\sqrt{3}}{\sqrt{r^{2}-rR+R^{2}}}
.
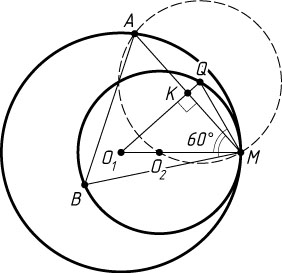
Второй способ. Пусть R\gt r
, O_{1}
и O_{2}
— центры окружностей, AMB
— равносторонний треугольник, M
— точка касания окружностей, A
— точка на большей окружности, B
— на меньшей.
Рассмотрим поворот вокруг точки M
, при котором точка B
переходит в точку A
. При этом повороте центр O_{2}
меньшей окружности перейдёт в некоторую точку Q
, причём \angle O_{1}MQ=60^{\circ}
, окружность с центром O_{2}
— в окружность того же радиуса r
с центром Q
, а так как отрезок AM
— общая хорда окружностей с центрами Q
и O_{1}
, то отрезок AM
делится прямой O_{1}Q
пополам и AM\perp O_{1}Q
. По теореме косинусов из треугольника O_{1}MQ
находим, что
O_{1}Q=\sqrt{r^{2}-rR+R^{2}}.
Пусть K
середина AM
. Тогда MK
— высота треугольника O_{1}MQ
. Выражая двумя способами площадь треугольника MQO_{1}
, получим, что
\frac{1}{2}O_{1}Q\cdot MK=\frac{1}{2}O_{1}M\cdot QM\cdot\sin\angle O_{1}MQ,
откуда находим, что
AM=2MK=\frac{2O_{1}M\cdot QM\cdot\sin\angle O_{1}MQ}{O_{1}Q}=\frac{rR\sqrt{3}}{\sqrt{r^{2}-rR+R^{2}}}.
Источник: Вступительный экзамен в МФТИ. — 1966, билет 4, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 66-4-2, с. 115
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 205, с. 24
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 205, с. 25
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.38, с. 70

