4773. Теорема Ньютона. Докажите, что во всяком описанном четырёхугольнике середины диагоналей и центр вписанной окружности расположены на одной прямой.
Указание. Геометрическим местом точек M
, лежащих внутри четырёхугольника ABCD
с непараллельными сторонами AB
и CD
, и таких, что сумма площадей треугольников ABM
и CDM
постоянна, является отрезок.
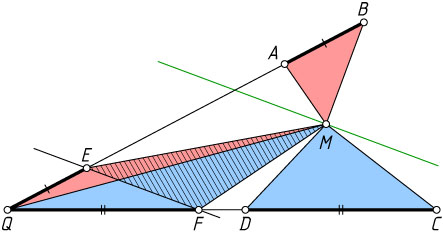
Решение. Докажем сначала следующее утверждение. Если на плоскости даны два отрезка AB
и CD
(AB
не параллельно CD
), то геометрическое место точек M
, расположенных внутри одного из углов, образованных прямыми AB
и CD
, и таких, что сумма площадей треугольников ABM
и CDM
постоянна, есть отрезок с концами на прямых AB
и CD
(рис. 1).
Действительно, пусть прямые AB
и CD
пересекаются в точке Q
. Отложим на сторонах угла AQD
отрезки QE
и QF
, равные соответственно AB
и CD
. Тогда
S_{\triangle QME}+S_{\triangle QMF}=S_{\triangle AMB}+S_{\triangle CMD}.
Поэтому S_{\triangle EMF}=\pm(S_{QEMF}-S_{\triangle QEF})
. Следовательно, площадь треугольника EMF
постоянна. Поэтому точка M
перемещается по прямой, параллельной EF
.
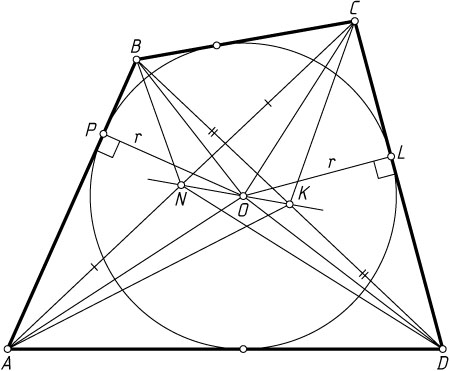
Пусть теперь ABCD
— описанный четырёхугольник (рис. 2), O
— центр вписанной окружности, r
— её радиус, N
и K
— середины диагоналей AC
и BD
соответственно. Тогда
S_{\triangle ANB}+S_{\triangle DNC}=\frac{1}{2}S_{\triangle ABC}+\frac{1}{2}S_{\triangle ADC}=\frac{1}{2}S_{ABCD}.
Аналогично S_{\triangle AKB}+S_{\triangle DKC}=\frac{1}{2}S_{ABCD}
.
Пусть P
и L
— точки касания вписанной окружности со сторонами AB
и CD
. Тогда
S_{\triangle AOB}+S_{\triangle COD}=\frac{1}{2}AB\cdot OP+\frac{1}{2}CD\cdot OL=
=r\cdot\frac{AB+CD}{2}=r\cdot\frac{AD+BC}{2}.
Поэтому S_{\triangle AOB}+S_{\triangle COD}=\frac{1}{2}S_{ABCD}
.
По ранее доказанному точки N
, O
и K
лежат на одной прямой.
Примечание. Более подробное изложение вопросов, связанных с теоремой Ньютона, см. в разделе «Замечательные теоремы и факты геометрии» (В.В.Прасолов, И.Ф.Шарыгин) книги «Факультативный курс по математике», составитель И.Л.Никольская (с.329).
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 210, с. 21
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 540, с. 66
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — № 6, с. 23
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 24, с. 201
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 116, с. 147
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 115, с. 37
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 329
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 57
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.5, с. 152
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — с. 537

