4789. Три окружности S_{1}
, S_{2}
и S_{3}
попарно касаются друг друга в трёх различных точках. Докажите, что прямые, соединяющие точку касания окружностей S_{1}
и S_{2}
с двумя другими точками касания, пересекают окружность S_{3}
в точках, являющихся концами её диаметра.
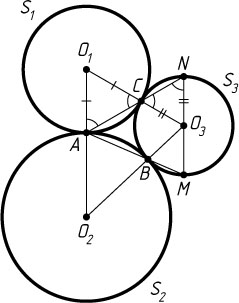
Указание. Пусть O_{1}
, O_{2}
и O_{3}
— центры данных окружностей, а M
и N
— точки пересечения указанных прямых с третьей окружностью. Докажите, что O_{3}M\parallel O_{1}O_{2}
и O_{3}N\parallel O_{1}O_{2}
.
Решение. Рассмотрим случай внешнего касания окружностей. Пусть окружности S_{1}
и S_{2}
касаются в точке A
, S_{2}
и S_{3}
— в точке B
, S_{1}
и S_{3}
— в точке C
; O_{1}
, O_{2}
, O_{3}
— центры этих окружностей.
Если прямые AB
и AC
пересекают окружность S_{3}
соответственно в точках M
и N
(отличных от B
и C
), то равнобедренные треугольники AO_{1}C
и NO_{3}C
имеют равные углы при вершине C
. Поэтому их углы при вершинах A
и N
также равны. Следовательно, O_{3}N\parallel O_{1}A
. Аналогично O_{3}M\parallel O_{2}A
.
Точка A
лежит на прямой O_{1}O_{2}
. Поэтому O_{3}N\parallel O_{1}O_{2}
и O_{3}M\parallel O_{1}O_{2}
. Следовательно, прямая MN
проходит через центр O_{3}
третьей окружности.
Аналогично для случая, когда две внешне касающиеся окружности касаются третьей внутренним образом.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.17, с. 60
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.18, с. 58
