4791. Радиусы окружностей S_{1}
и S_{2}
, касающихся в точке A
, равны R
и r
(R\gt r
). Найдите длину касательной, проведённой к окружности S_{2}
из точки B
, лежащей на окружности S_{1}
, если известно, что AB=a
. (Разберите случаи внутреннего и внешнего касания.)
Ответ. a\sqrt{1\pm\frac{r}{R}}
.
Указание. Примените теорему о касательной и секущей.
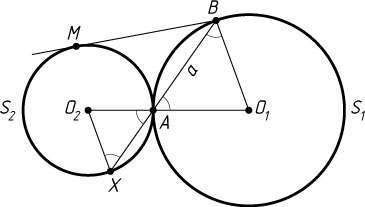
Решение. Рассмотрим случай внешнего касания. Пусть O_{1}
и O_{2}
— центры окружностей S_{1}
и S_{2}
; X
— точка пересечения прямой AB
с окружностью S_{2}
, отличная от A
; BM
— касательная к окружности S_{1}
(M
— точка касания).
Равнобедренные треугольники XO_{2}A
и BO_{1}A
подобны с коэффициентом \frac{r}{R}
, поэтому
AX=\frac{r}{R}\cdot AB=\frac{ar}{R}.
По теореме о касательной и секущей
BM^{2}=BX\cdot BA=(BA+AX)BA=\left(a+\frac{ar}{R}\right)a=a^{2}\left(1+\frac{r}{R}\right).
Следовательно, BM=a\sqrt{1+\frac{r}{R}}
.
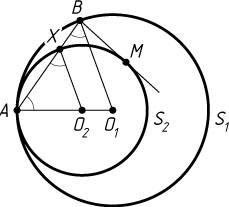
В случае внутреннего касания аналогично получим, что
BM=a\sqrt{1-\frac{r}{R}}.
