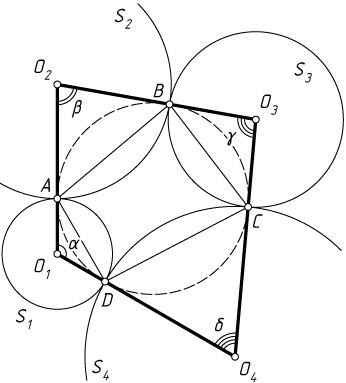
4792. Даны четыре окружности, каждая из которых касается внешним образом двух из трёх остальных. Докажите, что через точки касания можно провести окружность.
Указание. Выразите противоположные углы четырёхугольника с вершинами в точках касания через углы четырёхугольника с вершинами в центрах данных окружностей.
Решение. Первый способ. Пусть A
, B
, C
и D
— точки касания окружностей S_{1}
и S_{2}
, S_{2}
и S_{3}
, S_{3}
и S_{4}
, S_{4}
и S_{1}
; O_{1}
, O_{2}
, O_{3}
, O_{4}
соответственно — центры этих окружностей.
Поскольку окружности касаются внешним образом, никакие три из точек O_{1}
, O_{2}
, O_{3}
, O_{4}
не лежат на одной прямой. Обозначим углы четырёхугольника O_{1}O_{2}O_{3}O_{4}
при вершинах O_{1}
, O_{2}
, O_{3}
, O_{4}
через \alpha
, \beta
, \gamma
и \delta
соответственно. Тогда
\alpha+\beta+\gamma+\delta=360^{\circ}.
С другой стороны,
\angle DAB=180^{\circ}-\angle DAO_{1}-\angle BAO_{2}=180^{\circ}-\left(90^{\circ}-\frac{\alpha}{2}\right)-\left(90^{\circ}-\frac{\beta}{2}\right)=\frac{\alpha+\beta}{2}.
Аналогично \angle DCB=\frac{\gamma+\delta}{2}
. Поэтому
\angle DAB+\angle DCB=\frac{\alpha+\beta+\gamma+\delta}{2}=180^{\circ}.
Следовательно, четырёхугольник ABCD
— вписанный.
Второй способ. Пусть A
, B
, C
и D
— точки касания окружностей S_{1}
и S_{2}
, S_{2}
и S_{3}
, S_{3}
и S_{4}
, S_{4}
и S_{1}
соответственно. Поскольку окружности касаются внешним образом, любые три точки касания не лежат на одной прямой.
При инверсии с центром в точке A
окружности S_{1}
и S_{2}
, проходящие через центр инверсии, перейдут в параллельные прямые a_{1}
и a_{2}
, а окружности S_{3}
и S_{4}
, не проходящие через центр инверсии, — в касающиеся между собой в некоторой точке C'
окружности S_{3}'
и S_{4}'
. При этом окружность S_{4}'
будет касаться прямой a_{1}
в некоторой точке D'
, окружность S_{3}'
— прямой a_{2}
в некоторой точке B'
.
Окружности S_{3}'
и S_{4}'
гомотетичны относительно точки касания C'
. При этой гомотетии касательная a_{2}
к окружности S_{3}'
переходит в параллельную ей касательную a_{1}
к окружности S_{4}'
, а точка касания B'
— в точку касания D'
. Поэтому точки B'
, C'
и D'
лежат на одной прямой. При инверсии с центром A
эта прямая перейдёт либо в себя (что невозможно, так как точки B
, C
и D
не лежат на одной прямой), либо в окружность, проходящую через центр A
инверсии. Следовательно, точки B
, C
, D
и A
лежат на этой окружности. Что и требовалось доказать.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — № 216, с. 185
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.22, с. 60
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.23, с. 58
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 7.6, с. 58; с. 262
