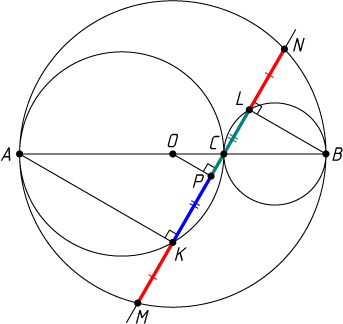
4793. На отрезке AB
взята точка C
. Прямая, проходящая через точку C
, пересекает окружности с диаметрами AC
и BC
в точках K
и L
, а также окружность с диаметром AB
— в точках M
и N
. Докажите, что KM=LN
.
Указание. Пусть X_{1}Y_{1}
— проекция отрезка XY
на прямую l
, а M
— середина отрезка XY
. Тогда проекция точки M
на прямую l
— середина отрезка X_{1}Y_{1}
.
Решение. Пусть P
— проекция центра O
окружности с диаметром AB
на хорду MN
этой окружности. Поскольку \angle AKC=\angle BLC=90^{\circ}
, то K
и L
— проекции точек A
и B
на хорду MN
, а так как O
— середина AB
, то P
— середина KL
. Кроме того, точка P
делит хорду MN
пополам. Следовательно, KM=LN
.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.22, с. 58
