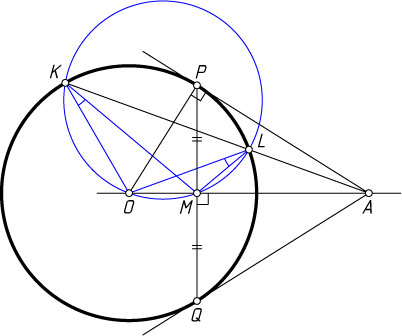
4796. На продолжении хорды KL
окружности с центром O
взята точка A
, и из неё проведены касательные AP
и AQ
(P
и Q
— точки касания); M
— середина отрезка PQ
. Докажите, что:
а) \angle MKO=\angle MLO
;
б) \angle KMP=\angle LMP
.
Указание. Из равенства AO\cdot AM=AK\cdot AL
следует, что точки K
, L
, M
и O
лежат на одной окружности.
Решение. а) Докажем, что точки K
, L
, M
и O
лежат на одной окружности. Отсюда будет следовать равенство указанных углов.
Заметим, что точки A
, M
и O
лежат на одной прямой. Поскольку PM
— высота прямоугольного треугольника APO
, проведённая из вершины P
прямого угла, то AP^{2}=AO\cdot AM
. С другой стороны, по теореме о касательной и секущей AP^{2}=AK\cdot AL
. Поэтому
AO\cdot AM=AK\cdot AL.
Следовательно, точки K
, L
, M
и O
лежат на одной окружности (см. задачу 114). Что и требовалось доказать.
б) Точки K
, L
, M
и O
лежат на одной окружности (см. пункт а)). Пусть луч MP
пересекает эту окружность в точке T
. Поскольку TM\perp MO
, отрезок OT
— диаметр окружности. Кроме того, прямая OT
проходит через центры двух пересекающихся окружностей, значит, точка T
— середина дуги KTL
окружности, проходящей через точки K
, L
, M
и O
. Следовательно,
\angle KMP=\angle KMT=\angle LMT=\angle LMP.
(Можно и так. Четырёхугольник OMKL
вписанный, а треугольник KOL
равнобедренный, поэтому
\angle AML=\angle LKO=\angle KLO=\angle KMO.
Следовательно,
\angle LMP=90^{\circ}-\angle AML=90^{\circ}-\angle KMO=\angle KMP.)
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.29, с. 62
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.30, с. 60
