4798. Точка X
движется по окружности с центром O
. На каждом радиусе OX
откладывается отрезок OM
, длина которого равна расстоянию от точки X
до заданного диаметра окружности. Найдите геометрическое место точек M
.
Ответ. Две равные касающиеся окружности.
Указание. Пусть CD
— диаметр окружности, перпендикулярный данному диаметру AB
. Используя признаки равенства треугольников, докажите, что радиус OC
(или OD
) виден из точки M
под прямым углом.
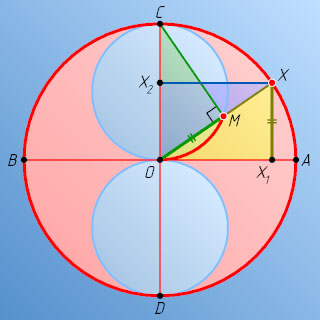
Решение. Пусть CD
— диаметр данной окружности, перпендикулярный данному диаметру AB
, X
— произвольная точка дуги AC
, X_{1}
и X_{2}
— проекции точки X
на AB
и OC
соответственно. Тогда
OC=OX,~OM=XX_{1}=OX_{2}.
Поэтому треугольники CMO
и XX_{2}O
равны по двум сторонам и углу между ними. Значит,
\angle CMO=\angle XX_{2}O=90^{\circ}.
Следовательно, точка M
лежит на окружности с диаметром OC
. Аналогично, для любой другой точки данной окружности.
Докажем теперь, что каждая точка этих окружностей удовлетворяет условию задачи.
Рассмотрим произвольную точку N
окружности с диаметром OC
. Пусть X
— точка пересечения луча ON
с исходной окружностью, X_{1}
и X_{2}
— проекции точки X
на AB
и OC
соответственно. Тогда прямоугольные треугольники CNO
и XX_{2}O
равны по гипотенузе и острому углу. Следовательно,
ON=OX_{2}=XX_{1}.
Аналогично для любой точки окружности с диаметром OD
.
