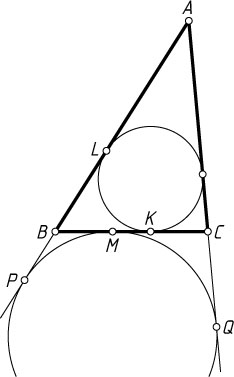
4805. Окружность касается стороны BC
треугольника ABC
в точке M
, а продолжений сторон AB
и AC
— в точках P
и Q
соответственно. Вписанная окружность треугольника ABC
касается стороны BC
в точке K
, а стороны AB
— в точке L
. Докажите, что:
а) отрезок AP
равен полупериметру p
треугольника ABC
;
б) BM=CK
;
в) BC=PL
.
Указание. Отрезки касательных, проведённых к окружности из одной точки, равны между собой.
Если окружность, вписанная в треугольник PQR
, касается стороны PQ
в точке S
, а p
— полупериметр треугольника, то PS=p-RQ
.
Решение. а) Поскольку BP=BM
, CQ=CM
и AP=AQ
, то
AB+BC+AC=AB+(BM+MC)+AC=
=AB+(BP+QC)+AC=(AB+BP)+(QC+AC)=AP+AQ=2AP.
Следовательно,
AP=\frac{AB+BC+AC}{2}=p.
б)
BM=BP=AP-AB=p-AB=CK.
в)
PL=AP-AL=p-(p-BC)=BC.
Примечание. См. также статью А.Блинкова и Ю.Блинкова «Вневписанная окружность», Квант, 2009, N2, с.34-37, 45.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 90(а), с. 95
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 228, с. 23
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 16
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 25, с. 10
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 63, с. 144
