4816. Окружности радиусов 8 и 3 касаются внутренним образом. Из центра большей окружности проведена касательная к меньшей окружности. Найдите длину этой касательной.
Ответ. 4.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
Решение. Пусть O
и O_{1}
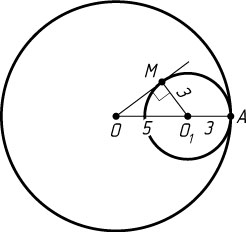
— центры окружностей радиусов 8 и 3 соответственно, A
— точка касания окружностей, OM
— искомая касательная. Тогда
OO_{1}=OA-OO_{1}=8-3=5.
Следовательно,
OM^{2}=OO^{2}_{1}-O_{1}M^{2}=25-9=16,OM=4.
Источник: Вступительный экзамен в МИНХ. — 1988, № 14
Источник: Журнал «Квант». — 1989, № 5, с. 73
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.4, с. 67
