4818. Две окружности касаются друг друга внешним образом. Четыре точки A
, B
, C
и D
касания их общих внешних касательных последовательно соединены. Докажите, что в четырёхугольник ABCD
можно вписать окружность и найдите её радиус, если радиусы данных окружностей равны R
и r
.
Ответ. \frac{2rR}{R+r}
.
Указание. Проведите общую внутреннюю касательную.
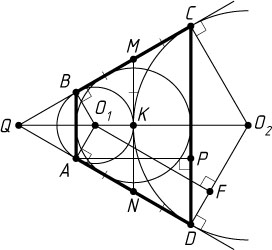
Решение. Пусть AD
и BC
— общие касательные к окружностям радиусов r
и R
(r\lt R
) с центрами в точках O_{1}
и O_{2}
соответственно; точки A
и B
лежат на первой окружности, C
и D
— на второй.
Если Q
— точка пересечения прямых AD
и BC
, то QAB
и QDC
— равнобедренные треугольники. Следовательно, AB
параллельно CD
и ABCD
— равнобедренная трапеция.
Пусть общая внутренняя касательная пересекает отрезки BC
и AD
в точках M
и N
соответственно. Если K
— точка касания окружностей, то
MK=KN,~AN=NK=ND,~BM=MK=MC.
Поэтому MN
— средняя линия трапеции ABCD
и
AD+BC=2MN=AB+DC.
Следовательно, в трапецию ABCD
можно вписать окружность.
Пусть F
— проекция точки O_{1}
на O_{2}D
. Тогда (см. задачу 365)
O_{1}O_{2}=R+r,~O_{2}F=R-r,~O_{1}F=2\sqrt{rR}.
Пусть P
— проекция точки A
на DC
. Тогда треугольник APD
подобен треугольнику O_{1}FO_{2}
по двум углам. Поэтому
AP=AD\cdot\frac{O_{1}F}{O_{1}O_{2}}=\frac{4rR}{r+R}.
Следовательно, искомый радиус равен \frac{2rR}{r+R}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.378, с. 184
