4826. Радиус окружности, описанной около прямоугольного треугольника, относится к радиусу вписанной в него окружности как 5:2
. Найдите площадь треугольника, если один из его катетов равен a
.
Ответ. \frac{3}{8}a^{2}
или \frac{2}{3}a^{2}
.
Указание. Выразите гипотенузу и второй катет треугольника через a
и радиус вписанной окружности, и воспользуйтесь теоремой Пифагора.
Решение. Обозначим через R
и r
радиусы описанной и вписанной окружностей соответственно. Тогда R=\frac{5}{2}r
. Поэтому гипотенуза равна 5r
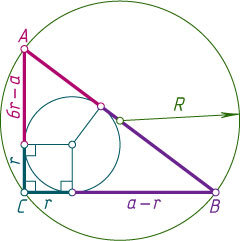
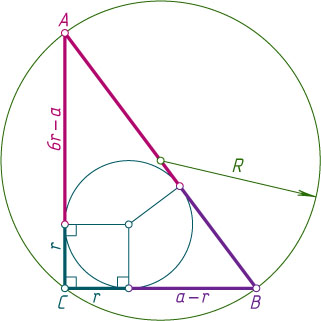
. Из равенства отрезков касательных, проведённых к окружности из одной точки, следует, что второй катет равен 7r-a
. По теореме Пифагора
a^{2}+(7r-a)^{2}=25r^{2},~\mbox{или}~12r^{2}-7ar+a^{2}=0.
Отсюда находим, что r=\frac{a}{4}
или r=\frac{a}{3}
. Зная радиус вписанной окружности, найдём второй катет и вычислим площадь треугольника.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.188, с. 171

