4832. Задача об арбелосе Архимеда. Точка C
расположена на отрезке AB
. По одну сторону от прямой AB
на отрезках AB
, AC
и BC
построены как на диаметрах полуокружности S
, S_{1}
и S_{2}
. Через точку C
проведена прямая CD
, перпендикулярная AB
(D
— точка на полуокружности S
). Окружность K_{1}
касается отрезка CD
и полуокружностей S
и S_{1}
, а окружность K_{2}
— отрезка CD
и полуокружностей S
и S_{2}
. Докажите, что окружности K_{1}
и K_{2}
равны.
Указание. Выразите радиусы окружностей K_{1}
и K_{2}
через радиусы полуокружностей S_{1}
и S_{2}
или рассмотрите инверсию относительно окружности с центром B
радиуса BD
.
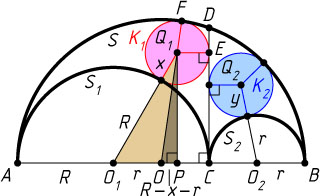
Решение. Первый способ. Пусть O
— центр полуокружности S
, O_{1}
, O_{2}
— центры полуокружностей S
(рис. 1), S_{1}
и S_{2}
, R
и r
— их радиусы (тогда радиус полуокружности S
равен R+r
), R\gt r
; Q_{1}
и Q_{2}
— центры окружностей K_{1}
и K_{2}
, x
и y
— их радиусы; F
и E
— точки касания окружности K_{1}
с полуокружностью S
и с отрезком CD
; P
— проекция точки Q_{1}
на AB
. В треугольнике OQ_{1}O_{1}
известно, что
O_{1}Q_{1}=R+x,~OQ_{1}=OF-Q_{1}F=R+r-x,
O_{1}O=OA-O_{1}A=R+r-R=r.
Поскольку PC=Q_{1}E=x
, то
O_{1}P=O_{1}C-PC=R-x,~OP=O_{1}P-OO_{1}=R-x-r.
Из прямоугольных треугольников O_{1}PQ_{1}
и OPQ_{1}
находим, что
PQ^{2}_{1}=O_{1}Q^{2}_{1}-O_{1}P^{2}=OQ^{2}_{1}-OP^{2},
или
(R+x)^{2}-(R-x)^{2}=(R+r-x)^{2}-(R-r-x)^{2}.
Из этого уравнения находим, что x=\frac{Rr}{R+r}
. Аналогично находим, что y=\frac{Rr}{R+r}
.
Второй способ. Обозначим окружности, полуокружностями которых являются S
, S_{1}
и S_{2}
, теми же буквами, что и в первом способе. Остальные обозначения также оставим без изменения.
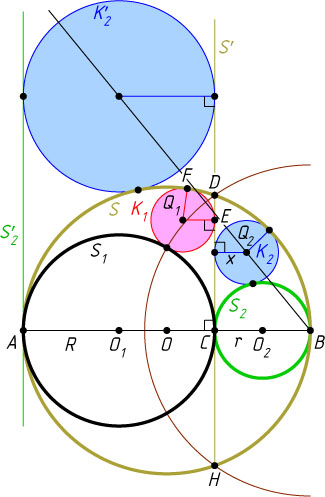
Рассмотрим инверсию относительно окружности с центром B
радиуса BD
(рис. 2). Если прямая DC
вторично пересекает окружность S
в точке H
, то окружность S
, проходящая через центр B
инверсии, переходит в прямую DH
, так как точки D
и H
, лежащие на окружности инверсии, остаются на месте.
Точка C
переходит в A
, так как BA\cdot BC=BD^{2}
, поэтому окружность S_{2}
, также проходящая через центр инверсии, переходит в прямую S_{2}'
, параллельную CD
и проходящую через точку A
.
Окружность K_{2}
, не проходящая через центр инверсии и касающаяся окружностей S
и S_{2}
, переходит в окружность K_{2}'
, касающуюся параллельных прямых CD
и S_{2}'
, поэтому радиус окружности K_{2}'
равен R
.
Окружность K_{2}'
гомотетична окружности K_{2}
, причём центр гомотетии совпадает с центром инверсии B
(см. задачу 6131). При этой гомотетии касательная CE
к окружности K_{2}
переходит в параллельную ей касательную S_{2}'
к окружности S_{1}
, значит, точка C
переходит в точку A
, а коэффициент гомотетии равен \frac{AB}{BC}=\frac{2R+2r}{2r}=\frac{R+r}{r}
. Следовательно, если x
— радиус окружности K_{2}
, то \frac{R}{x}=\frac{R+r}{r}
, откуда находим, что x=\frac{rR}{r+R}
.
Аналогично, радиус окружности K_{1}
также равен \frac{rR}{r+R}
(формула симметрична относительно r
и R
).
Примечание. См. также статью Л.Шибасова «Две задачи Архимеда», Квант, 2000, N1, с.41-42, 54.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — № 215(а), с. 185
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 327
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 562, с. 69
Источник: Жижилкин И. Д. Инверсия. — (Библиотека «Математическое просвещение». Вып. 35). — М.: МЦНМО, 2009. — с. 23
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 12.66, с. 306
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 12.68, с. 294

