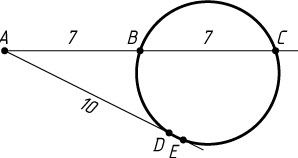
4839. Из точки A
проведены два луча, пересекающие данную окружность: один — в точках B
и C
, другой — в точках D
и E
. Известно, что AB=7
, BC=7
, AD=10
. Найдите DE
.
Ответ. \frac{1}{5}
.
Указание. Примените следствие из теоремы о касательной и секущей.
Решение. Ясно, что точка B
расположена между точками A
и C
. Предположим, что точка D
расположена между точками A
и E
. Тогда по следствию из теоремы о касательной и секущей
AB\cdot AC=AD\cdot AE,~\mbox{или}~14\cdot7=10(10+DE).
Отсюда находим, что DE=-\frac{1}{5}
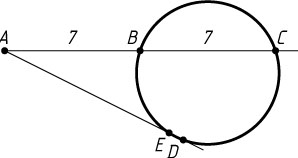
, что невозможно. Поэтому точка E
расположена между A
и D
. Тогда
AB\cdot AC=AD\cdot AE,~\mbox{или}~14\cdot7=10(10-DE).
Отсюда находим, что DE=\frac{1}{5}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 16.027, с. 349
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.5, с. 93

