4841. Из центра каждой из двух данных окружностей проведены касательные к другой окружности. Докажите, что хорды, соединяющие точки пересечения касательных с окружностями (см.рис.), равны.
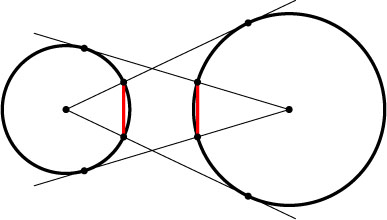
Указание. Выразите каждую из указанных хорд через радиусы окружностей и расстояние между их центрами.
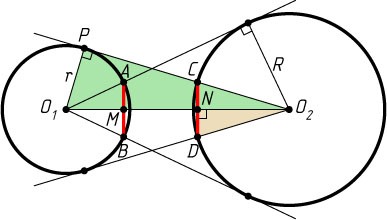
Решение. Пусть O_{1}
и O_{2}
— центры окружностей; r
и R
— их радиусы, AB
и CD
— указанные хорды; M
и N
— их точки пересечения с отрезком O_{1}O_{2}
; O_{2}P
— касательная к первой окружности (P
— точка касания). Ясно, что M
и N
— середины этих хорд.
Из подобия прямоугольных треугольников O_{2}ND
и O_{2}PO_{1}
находим, что
DN=O_{1}P\cdot\frac{O_{2}D}{O_{1}O_{2}}=\frac{rR}{O_{1}O_{2}}.
Поэтому DC=\frac{2rR}{O_{1}O_{2}}
. Аналогично докажем, что AB=\frac{2rR}{O_{1}O_{2}}
.
Автор: Савин А. П.
Источник: Журнал «Квант». — 1981, № 10, с. 32, М706
Источник: Задачник «Кванта». — М706
Источник: Журнал «Crux Mathematicorum». — 1975, № 10, задача 63, с. 99

