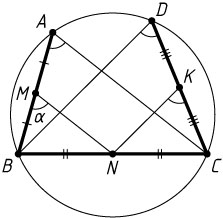
4843. В круге провели три хорды AB
, BC
, CD
и отметили их середины M
, N
и K
соответственно. Докажите, что \angle BMN=\angle NKC
или \angle BMN+\angle NKC=180^{\circ}
.
Указание. Отрезки KN
и MN
— средние линии треугольников BCD
и CBA
.
Решение. Пусть точки A
и D
лежат по одну сторону от прямой BC
. Поскольку KN
и MN
— средние линии треугольников BCD
и CBA
, то KN\parallel BD
и MN\parallel AC
. Поэтому
\angle NKC=\angle BDC=\angle BAC=\angle BMN.
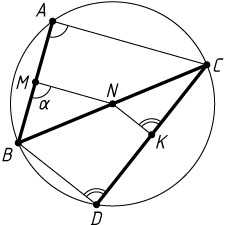
Пусть точки A
и D
лежат по разные стороны от прямой BC
. Поскольку KN
и MN
— средние линии треугольников BCD
и CBA
, то KN\parallel BD
и MN\parallel AC
. Поэтому
\angle BMN=\angle BAC,~\angle NKC=\angle BDC.
Следовательно,
\angle BMN+\angle NKC=\angle BAC+\angle BDC=180^{\circ}.
Автор: Гальперин Г. А.
Источник: Журнал «Квант». — 1986, № 11, с. 33, задача 5
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 100

