4850. На плоскости даны три окружности одинакового радиуса. Докажите, что если все они пересекаются в одной точке, как показано на рисунке, то сумма отмеченных дуг AK
, CK
и EK
равна 180^{\circ}
.
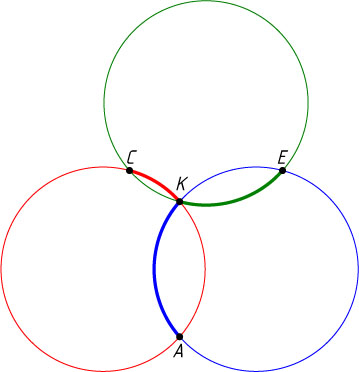
Ответ. Соедините центры окружностей с точками A
, C
и E
.
Решение. Пусть O_{1}
, O_{2}
, O_{3}
— центры указанных окружностей. Обозначим
\angle CO_{1}K=\alpha,~\angle AO_{2}K=\beta,~\angle EO_{3}K=\gamma.
Докажем, что \alpha+\beta+\gamma=180^{\circ}
.
Четырёхугольники CO_{1}KO_{3}
, AO_{2}KO_{1}
и EO_{3}KO_{2}
— ромбы. Поэтому
KO_{1}=O_{3}C,~KO_{1}\parallel O_{3}C,~KO_{2}=O_{3}E,~KO_{2}\parallel O_{3}E,
\angle O_{1}KO_{2}=\angle CO_{3}E=\alpha+\beta.
Следовательно,
180^{\circ}=\angle O_{1}KO_{2}+\angle AO_{1}K=\alpha+\beta+\gamma.
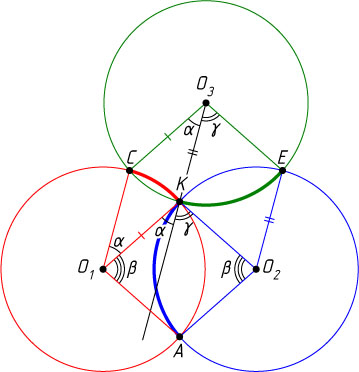
Источник: Журнал «Квант». — 1976, № 8, с. 36, М397(а)
Источник: Задачник «Кванта». — М397(а)

