4851. На плоскости даны три окружности одинакового радиуса. Докажите, что если они расположены так, как показано на рисунке, то сумма отмеченных дуг AB
, CD
и EF
равна 180^{\circ}
.
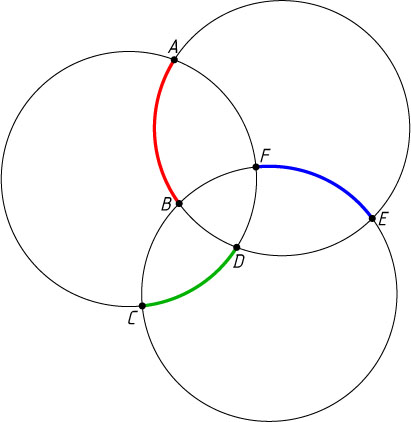
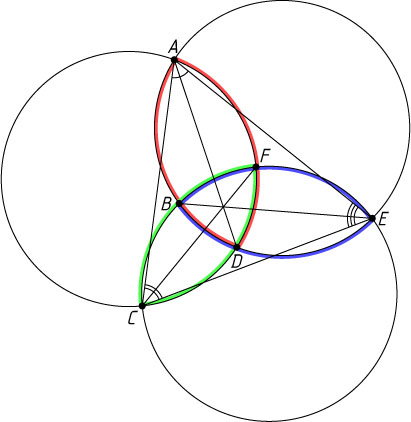
Указание. Докажите, что \smile AB+\smile CD+\smile EF=\smile AF+\smile BC+\smile DE
и сложите углы треугольника AEC
.
Решение. Поскольку \smile ABD=\smile AFD
, \smile CDF=\smile CBF
и \smile BFE=\smile BDE
, то
\smile AB+\smile CD+\smile EF=
=(\smile ABD-\smile BD)+(\smile CDF-\smile DF)+(\smile BFE-\smile BF)=
=(\smile AFD-\smile DF)+(\smile CBF-\smile BF)+(\smile EDB-\smile BD)=
=\smile AF+\smile BC+\smile DE.
В треугольнике AEC
известно, что
\angle CAE=\frac{1}{2}(\smile CD+\smile DE),~\angle ACE=\frac{1}{2}(\smile AF+\smile EF),~\angle AEC=\frac{1}{2}(\smile BC+\smile AB).
Следовательно,
180^{\circ}=\angle CAE+\angle ACE+\angle AEC=
=\frac{1}{2}(\smile CD+\smile DE+\smile AF+\smile EF+\smile BC+\smile AB)=
=\frac{1}{2}((\smile AB+\smile CD+\smile EF)+(\smile AF+\smile BC+\smile DE))=
=\frac{1}{2}\cdot2(\smile AB+\smile CD+\smile EF),
откуда следует, что
\smile AB+\smile CD+\smile EF=180^{\circ}.
Источник: Журнал «Квант». — 1976, № 8, с. 36, М397
Источник: Задачник «Кванта». — М397

