4856. Внутри треугольника расположены окружности \alpha
, \beta
, \gamma
, \delta
одинакового радиуса, причём каждая из окружностей \alpha
, \beta
, \gamma
касается двух сторон треугольника и окружности \delta
(см.рис.). Докажите, что центр окружности \delta
принадлежит прямой, проходящей через центры вписанной и описанной окружностей данного треугольника.
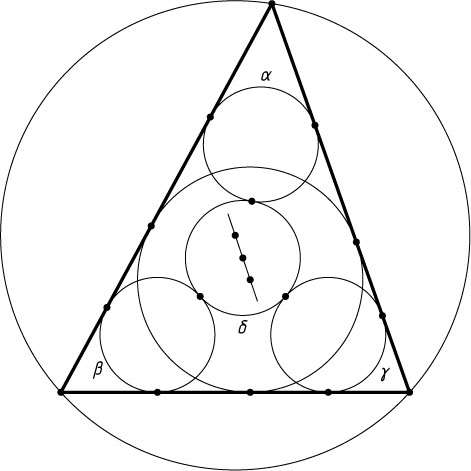
Указание. Треугольник с вершинами в центрах окружностей \alpha
, \beta
, \gamma
гомотетичен данному треугольнику.
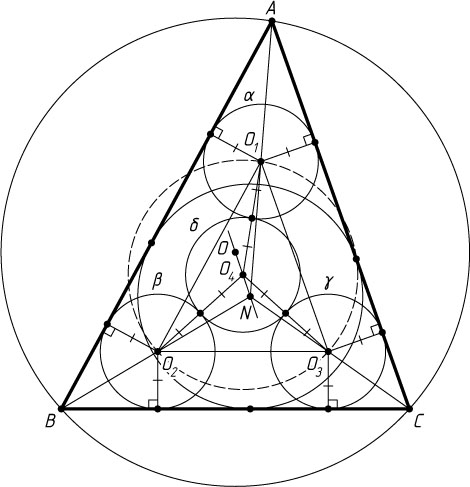
Решение. Пусть ABC
— данный треугольник; O_{1}
, O_{2}
, O_{3}
, O_{4}
— центры равных окружностей \alpha
, \beta
, \gamma
, \delta
соответственно; x
— радиус этих окружностей. Докажем, что треугольник O_{1}O_{2}O_{3}
гомотетичен треугольнику ABC
.
Действительно, стороны треугольника O_{1}O_{2}O_{3}
соответственно параллельны сторонам треугольника ABC
. При гомотетии с центром в точке N
, центре вписанной окружности треугольника O_{1}O_{2}O_{3}
(и треугольника ABC
), и коэффициентом, равным отношению расстояний от точки N
до прямых BC
и O_{2}O_{3}
, треугольник O_{1}O_{2}O_{3}
перейдёт в треугольник ABC
.
При этой гомотетии центр O_{4}
описанной окружности треугольника O_{1}O_{2}O_{3}
(O_{4}O_{1}=O_{4}O_{2}=O_{4}O_{3}=2x
) перейдёт в центр O
описанной окружности треугольника ABC
. Следовательно, точки N
, O_{4}
и O
лежат на одной прямой.
Примечание. Пусть радиусы вписанной и описанной окружностей данного треугольника равны r
и R
соответственно. Тогда радиусы четырёх равных окружностей, о которых говорится в условии задачи, равны \frac{Rr}{R+4r}
.