4858. В окружность вписан прямоугольник ABCD
, сторона AB
которого равна a
. Из конца K
диаметра KP
, параллельного стороне AB
, сторона BC
видна под углом \beta
. Найдите радиус окружности.
Ответ. \frac{a}{2|\cos\beta|}
.
Указание. \angle BAC=\beta
или \angle BAC=180^{\circ}-\beta
.
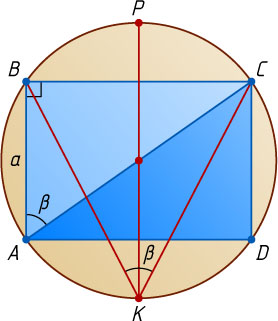
Решение. Пусть R
— искомый радиус. Рассмотрим случай, когда точка K
лежит на дуге AD
, не содержащей точки B
. Тогда в прямоугольном треугольнике ABC
известно, что
\angle BAC=\angle BKC=\beta,~2R=AC=\frac{AB}{\cos\angle BAC}=\frac{a}{\cos\beta}.
Следовательно, R=\frac{a}{2\cos\beta}
.
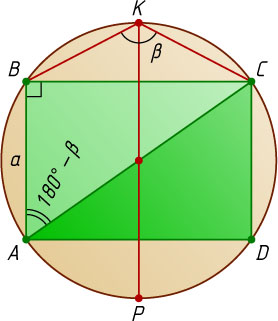
Если точка K
лежит на дуге ABD
, то аналогично найдём, что
R=-\frac{a}{2\cos\beta}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1964
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.8, с. 103

