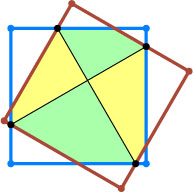
4871. Два квадрата в пересечении дают восьмиугольник (см.рис.). Две диагонали этого восьмиугольника делят его на четыре четырёхугольника. Докажите, что эти диагонали перпендикулярны.
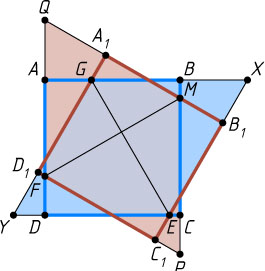
Решение. (Решение В.Радионова.) Пусть сторона BC
квадрата ABCD
и сторона A_{1}B_{1}
квадрата A_{1}B_{1}C_{1}D_{1}
(рис. 1) пересекаются в точке M
, стороны CD
и B_{1}C_{1}
— в точке E
, стороны AD
и C_{1}D_{1}
— в точке F
, стороны AB
и A_{1}D_{1}
— в точке G
. Докажем, что MF\perp EG
.
Пусть прямые BC
и C_{1}D_{1}
пересекаются в точке P
, прямые AD
и A_{1}B_{1}
— в точке Q
, прямые AB
и B_{1}C_{1}
— в точке X
, прямые CD
и A_{1}D_{1}
— в точке Y
. Тогда четырёхугольники MPFQ
и EXGY
— равные параллелограммы (их высоты соответственно равны и равны соответствующие острые углы), причём отрезки MF
и EG
— их соответствующие диагонали.
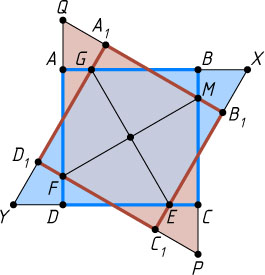
При параллельном переносе каждого из данных квадратов параллелограммы переходят в равные им параллелограммы (рис. 2). С помощью таких переносов можно добиться того, что центры полученных квадратов совпадают. Полученные при этом параллелограммы равны, а их стороны соответственно перпендикулярны, поэтому при повороте на угол 90^{\circ}
относительно общего центра полученных квадратов один параллелограмм переходит в другой. Тогда диагональ одного параллелограмма, соответствующая отрезку MF
, перейдёт в диагональ другого параллелограмма, соответствующую отрезку EG
. Следовательно, MF\perp EG
.
Примечание. (А.Сгибнев.) Утверждение легко усилить: указанные отрезки не только перпендикулярны, но и равны. Причём это прямо следует из приведённого решения.
Автор: Произволов В. В.
Источник: Журнал «Квант». — 1992, № 5, с. 33, задача 5


