4872. Диаметр AB
окружности равен 1. На нём отложен отрезок AC
, равный a
. Проведена также хорда AD
, равная b
. Из точки C
восстановлен перпендикуляр к AB
, пересекающий хорду AD
в точке E
, а из точки D
опущен перпендикуляр DF
на AB
(см.рис.). Оказалось, что AE=AF
. Докажите, что a=b^{3}
.
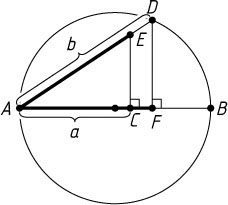
Указание. Рассмотрите подобные треугольники.
Решение. Треугольник ADB
— прямоугольный, \angle ADB=90^{\circ}
. Поэтому
AD^{2}=AF\cdot AB,~\mbox{или}~b^{2}=AF\cdot1=AF.
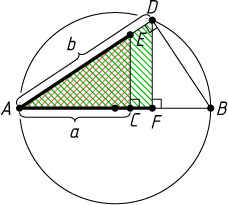
С другой стороны, из подобия прямоугольных треугольников AFD
и ACE
следует, что
\frac{AF}{AC}=\frac{AD}{AE},~\mbox{или}~\frac{AF}{a}=\frac{b}{AF}.
Значит, AF^{2}=ab
. Таким образом, b^{4}=ab
. Следовательно, a=b^{3}
.
Источник: Журнал «Квант». — 1992, № 8, с. 42, задача 3

