4876. На сторонах AB
и BC
равностороннего треугольника ABC
отмечены точки L
и K
соответственно, M
— точка пересечения отрезков AK
и CL
. Известно, что площадь треугольника AMC
равна площади четырёхугольника LBKM
. Найдите угол AMC
.
Ответ. 120^{\circ}
.
Указание. Треугольники BLC
и CKA
равны.
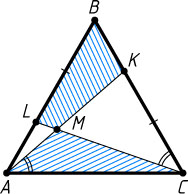
Решение. Первый способ. Заметим, что треугольники AKC
и CLB
равновелики (рис. 1), так как треугольник MKC
их общая часть, а четырёхугольник LBKM
равновелик треугольнику AMC
по условию.
Поскольку S_{\triangle AKC}=\frac{1}{2}AC\cdot CK\sin60^{\circ}
, а S_{\triangle CLB}=\frac{1}{2}BC\cdot BL\sin60^{\circ}
, причём AC=BC
, то из равенства S_{\triangle AKC}=S_{\triangle CLB}
следует, что CK=BL
. Тогда треугольники AKC
и CLB
равны по двум сторонам и углу между ними.
По теореме о внешнем угле треугольника
\angle AMC=\angle MKC+\angle MCK=\angle AKC+\angle BCL=\angle AKC+\angle CAK=
=180^{\circ}-\angle ACK=180^{\circ}-60^{\circ}=120^{\circ}.
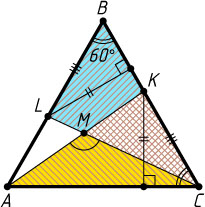
Второй способ. Поскольку
S_{\triangle BLC}=S_{BKML}+S_{\triangle KMC}=S_{\triangle AMC}+S_{\triangle KMC}=S_{\triangle AKC}
и BC=AC
(рис. 2), то высоты треугольников CLB
и AKC
, опущенные на их основания BC
и AC
, равны. Поэтому CK=BL
. Следовательно, треугольники CLB
и AKC
равны по двум сторонам и углу между ними. Значит,
\angle BLC+\angle BKM=\angle BLC+(180^{\circ}-\angle AKB)=
=\angle BLC+(180^{\circ}-\angle BLC)=180^{\circ}.
Значит, четырёхугольник BKML
вписанный. Следовательно,
\angle AMC=\angle KML=180^{\circ}-\angle KBL=180^{\circ}-60^{\circ}=120^{\circ}.
Примечание. Можно доказать, что треугольник BLC
получен из треугольника CKA
поворотом на угол 120^{\circ}
.
Автор: Произволов В. В.
Источник: Всероссийская олимпиада школьников. — 2012-2013, окружной тур, 10 класс

