4896. Окружности с центрами O_{1}
, O_{2}
, O_{3}
радиусов r_{1}
, r_{2}
, r_{3}
соответственно попарно касаются внешним образом. Общая внешняя касательная окружностей с центрами O_{1}
и O_{2}
параллельна общей внешней касательной окружностей с центрами O_{1}
и O_{3}
. Докажите, что r_{1}^{2}=4r_{2}r_{3}
.
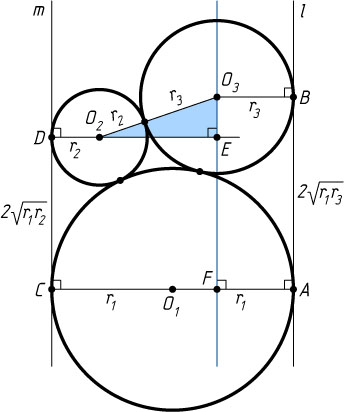
Решение. Рассмотрим случай, изображённый на рисунке (r_{3}\gt r_{2}
). Пусть прямая l
касается окружностей с центрами O_{1}
и O_{3}
в точках A
и B
соответственно, а прямая m
— окружностей с центрами O_{1}
и O_{2}
в точках соответственно C
и D
. Через точку O_{3}
проведём прямую, параллельную прямым l
и m
. Пусть эта прямая пересекает прямые AO_{1}
и DO_{2}
в точках F
и E
соответственно. Тогда AB=2\sqrt{r_{1}r_{3}}
и CD=2\sqrt{r_{1}r_{2}}
(см. задачу 365).
Рассмотрим прямоугольный треугольник O_{2}EO_{3}
со сторонами
O_{2}O_{3}=r_{2}+r_{3},~O_{2}E=AC-O_{2}D-O_{3}B=2r_{1}-r_{2}-r_{3},
O_{3}E=AB-CD=2\sqrt{r_{1}r_{3}}-2\sqrt{r_{1}r_{2}}.
По теореме Пифагора O_{2}O_{3}^{2}-O_{2}E^{2}=O_{3}E^{2}
, или
(r_{2}+r_{3})^{2}-(2r_{1}-r_{2}-r_{3})^{2}=(2\sqrt{r_{1}r_{2}}-2\sqrt{r_{1}r_{3}})^{2}~\Leftrightarrow
\Leftrightarrow~(r_{2}+r_{3}-2r_{1}+r_{2}+r_{3})(r_{2}+r_{3}+2r_{1}-r_{2}-r_{3})=4r_{1}(\sqrt{r_{2}}-\sqrt{r_{3}})^{2}~\Leftrightarrow
\Leftrightarrow~2(r_{2}+r_{3}-r_{1})\cdot2r_{1}=4r_{1}(r_{2}+r_{3}-2\sqrt{r_{2}r_{3}})~\Leftrightarrow
\Leftrightarrow~r_{2}+r_{3}-r_{1}=r_{2}+r_{3}-2\sqrt{r_{2}r_{3}}~\Leftrightarrow~r_{1}=2\sqrt{r_{2}r_{3}}~\Leftrightarrow~r_{1}^{2}=4r_{2}r_{3}.
Аналогично для r_{2}\geqslant r_{3}
.
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 335, с. 51
