4907. Основание равнобедренного треугольника равно 10, а боковая сторона равна 13. Отрезок с концами на боковых сторонах треугольника параллелен основанию и делится окружностью, вписанной в треугольник, в отношении 1:8:1
. Найдите длину этого отрезка.
Ответ. 5
или 8
.
Решение. Пусть BC=10
— основание равнобедренного треугольника ABC
, AB=AC=13
— боковые стороны, P
— точка касания вписанной окружности с боковой стороной AB
, M
и N
— точки на боковых сторонах AB
и AC
соответственно, причём MN\parallel BC
, K
и L
— точки пересечения этого отрезка с вписанной окружностью, MK:KL:LN=1:8:1
, E
— середина BC
.
Положим MK=LN=t
, KL=8t
. Тогда MN=10t
, коэффициент подобия треугольников AMN
и ABC
равен \frac{MN}{BC}=\frac{10t}{10}=t
, а AM=t\cdot AB=13t
.
Отрезки касательных, проведённых к окружности из одной точки, равны, поэтому
BP=BE=5,~AP=AB-BP=13-5=8.
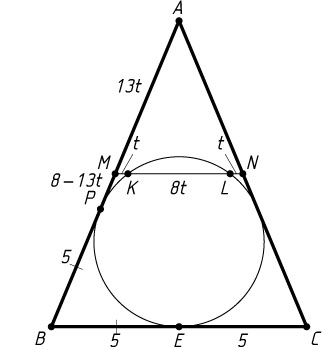
Если точка M
лежит между точками A
и P
(рис. 1), то
MP=AP-AM=8-13t\gt0.
По теореме о касательной и секущей MP^{2}=ML\cdot MK
, или
(8-13t)^{2}=9t^{2},~8-13t=3t,
откуда находим, что t=\frac{1}{2}
. Следовательно, MN=10t=5
.
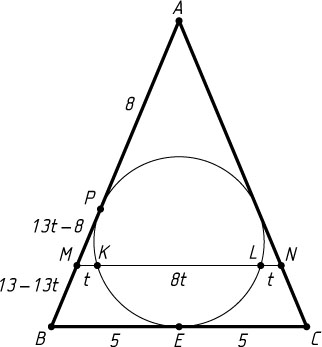
Если же точка M
лежит между B
и P
(рис. 2), то MP=AM-AP=13t-8\gt0
и аналогично находим, что t=\frac{4}{5}
. Следовательно, MN=10t=\frac{4}{5}\cdot10=8
.
Источник: ЕГЭ. — Задача C4, 2011

