4910. Точки P
, R
и Q
лежат на сторонах соответственно EF
, FG
и EG
треугольника EFG
, причём EPRQ
— параллелограмм, площадь которого составляет \frac{8}{25}
площади треугольника EFG
. Найдите диагональ PQ
параллелограмма, если известно, что EF=15
, EG=10
и \angle FEG=60^{\circ}
.
Ответ. 7
или 2\sqrt{31}
.
Решение. Пусть площадь треугольника QRG
равна S
, а \frac{RG}{FG}=k
. Треугольник QRG
подобен треугольнику EFG
с коэффициентом \frac{1}{k}
, а треугольник PFR
— треугольнику QRG
с коэффициентом \frac{1-k}{k}
, поэтому
S_{\triangle QRG}=\left(\frac{1}{k}\right)^{2}S_{\triangle EFG}=\left(\frac{1}{k}\right)^{2}S,~S_{\triangle PFR}=\left(\frac{1-k}{k}\right)^{2}S_{\triangle QRG}=\left(\frac{1-k}{k}\right)^{2}S,
S_{EPRQ}=S_{\triangle EFG}-S_{\triangle QRG}-S_{\triangle PFR}=\left(\frac{1}{k}\right)^{2}S-S-\left(\frac{1-k}{k}\right)^{2}S=\frac{8}{25}\left(\frac{1}{k}\right)^{2}S,
или
1-k^{2}-(1-k)^{2}=\frac{8}{25},~25k^{2}-25k+4=0,
откуда находим, что k=\frac{1}{5}
или k=\frac{4}{5}
.
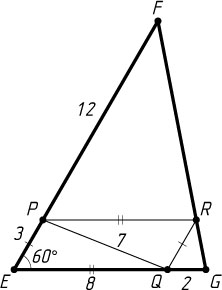
В первом из этих случаев (рис. 1)
EQ=PR=\frac{4}{5}EG=\frac{4}{5}\cdot10=8,~EP=QR=\frac{1}{5}EF=\frac{1}{5}\cdot15=3.
Следовательно,
PQ=\sqrt{EP^{2}+EQ^{2}-2EP\cdot EQ\cos60^{\circ}}=\sqrt{9+64-2\cdot3\cdot8\cdot\frac{1}{2}}=\sqrt{49}=7.
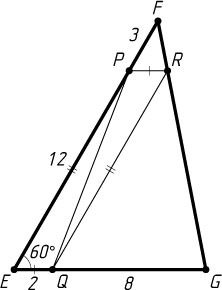
Во втором случае (рис. 2)
EQ=PR=\frac{1}{5}EG=\frac{1}{5}\cdot10=2,~EP=QR=\frac{4}{5}EF=\frac{4}{5}\cdot15=12,
Следовательно,
PQ=\sqrt{EP^{2}+EQ^{2}-2EP\cdot EQ\cos60^{\circ}}=\sqrt{144+4-2\cdot12\cdot2\cdot\frac{1}{2}}=\sqrt{124}=2\sqrt{31}.
Источник: ЕГЭ. — Задача C4, 2011

