4916. Окружность вписана в равнобедренную трапецию, большее основание которой равно 24, а синус угла при большем основании равен \frac{3}{5}
. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.
Ответ. \frac{1}{2}
или \frac{81}{130}
.
Решение. Пусть окружность радиуса R
с центром O
, вписанная в равнобедренную трапецию ABCD
с углом \alpha
при большем основании, касается боковой стороны AB
в точке M
, большего основания AD
в точке N
, причём AD=24
и \sin\alpha=\frac{3}{5}
. Тогда AM=AN=\frac{1}{2}AD=12
,
\sin\alpha=\frac{3}{5},~\cos\alpha=\frac{4}{5},~\tg\frac{\alpha}{2}=\frac{\sin\alpha}{1+\cos\alpha}=\frac{\frac{3}{5}}{1+\frac{4}{5}}=\frac{1}{3}.
Их прямоугольного треугольника AON
находим, что
R=ON=AN\tg\frac{\alpha}{2}=12\cdot\frac{1}{3}=4.
Пусть BT
— высота трапеции. Тогда
BT=2R=8,~AB=\frac{BT}{\sin\alpha}=\frac{8}{\frac{3}{5}}=\frac{40}{3},
BC=2BM=2\left(\frac{40}{3}-12\right)=\frac{8}{3}.
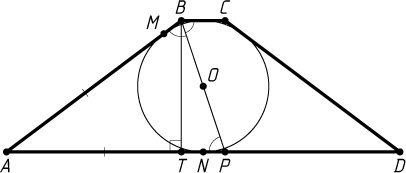
Пусть прямая, о которой говорится в условии задачи, проходит через вершину B
и пересекает основание AD
трапеции в точке P
(рис. 1). Тогда \angle APB=\angle CBP=\angle ABP
, значит, треугольник ABP
— равнобедренный, AP=AB=\frac{40}{3}
, поэтому
S_{\triangle ABP}=\frac{1}{2}AP\cdot BT=\frac{1}{2}AB\cdot BT=\frac{1}{2}\cdot\frac{40}{3}\cdot8=\frac{160}{3}.
Если S
— площадь трапеции ABCD
, то
S=\frac{1}{2}(AD+BC)BT=\frac{1}{2}(AB+CD)BT=\frac{1}{2}\cdot2AB\cdot BT=
=AB\cdot BT=\frac{40}{3}\cdot8=\frac{320}{3}
Следовательно, \frac{S_{\triangle ABP}}{S}=\frac{\frac{160}{3}}{\frac{320}{3}}=\frac{1}{2}
.
(Искомое отношение можно вычислить и так. Пусть K
— точка касания вписанной в трапецию окружности с основанием BC
. Тогда K
и N
— середины оснований, прямоугольные треугольники PON
и BOK
равны по катету и прилежащему острому углу, поэтому треугольник ABP
равновелик прямоугольной трапеции ABKN
. Следовательно, S_{\triangle ABP}=\frac{1}{2}S_{ABCD}
.)
Поскольку трапеция равнобедренная, для прямой, проходящей через вершину C
, получим тот же результат.
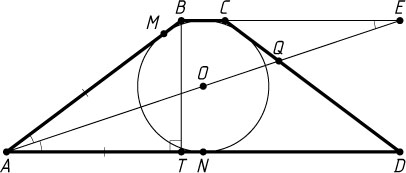
Пусть теперь указанная прямая проходит через вершину A
(рис. 2), пересекает боковую сторону CD
в точке Q
, а продолжение основания BC
— в точке E
. Треугольник ABE
— равнобедренный (\angle AEB=\angle DAE=\angle BAE
), поэтому
BE=AB=\frac{40}{3},~CE=BE-BC=AB-BC=\frac{40}{3}-\frac{8}{3}=\frac{32}{3}.
Треугольник AQD
подобен треугольнику EQC
с коэффициентом \frac{AD}{CE}=\frac{24}{\frac{32}{3}}=\frac{9}{4}
, значит, если QH
— высота треугольника AQD
, то
QH=\frac{9}{13}BT=\frac{9}{13}\cdot8=\frac{72}{13},~S_{\triangle AQD}=\frac{1}{2}AD\cdot QH=\frac{1}{2}\cdot24\cdot\frac{72}{13}=\frac{12\cdot72}{13}.
Следовательно, \frac{S_{\triangle AQD}}{S}=\frac{\frac{12\cdot72}{13}}{\frac{320}{3}}=\frac{81}{130}
.
Тот же результат для прямой, проходящей через вершину D
.
Источник: ЕГЭ. — Задача C4, 2011
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 17, с. 171

