4918. Дан квадрат ABCD
со стороной 7 и окружность S
с центром A
радиуса 2. Найдите радиус окружности, касающейся внешним образом окружности S
, содержащейся внутри квадрата и касающейся двух его соседних сторон.
Ответ. 3 или 16-9\sqrt{2}
.
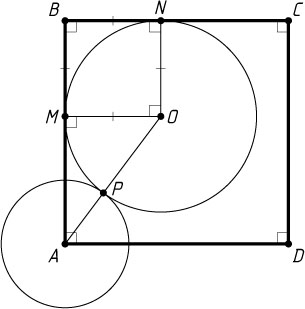
Решение. Пусть O
— центр искомой окружности, r
— её радиус, M
и N
— точки её касания со сторонами AB
и BC
соответственно (рис. 1), P
— точка касания с окружностью S
.
Линия центров касающихся окружностей проходит через их точку касания, поэтому AO=AP+OP=r+2
. Четырёхугольник OMBN
— квадрат, поэтому MB=ON=r
, AM=AB-MB=7-r
. По теореме Пифагора AO^{2}=OM^{2}+AM^{2}
, или
(r+2)^{2}=r^{2}+(7-r)^{2},~r^{2}-18r+45=0,
откуда находим, что r=3
или r=15
. Второе решение не удовлетворяет условию задачи, так как диаметр искомой окружности не может быть больше стороны данного квадрата.
Если искомая окружность касается сторон AD
и CD
, то её радиус также равен 3.
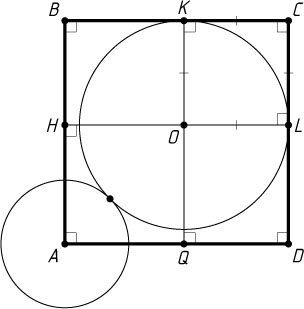
Пусть искомая окружность касается сторон BC
и CD
данного квадрата в точках K
и L
соответственно (рис. 2), Q
и H
— проекции точки O
на AD
и AB
соответственно. Тогда CKOL
и AQOH
— квадраты со сторонами r
и 7-r
, поэтому r+2=(7-r)\sqrt{2}
, откуда
r=\frac{7\sqrt{2}-2}{\sqrt{2}+1}=16-9\sqrt{2}.
Тогда 2r=32-18\sqrt{2}\lt9
, значит, это решение удовлетворяет условию задачи.
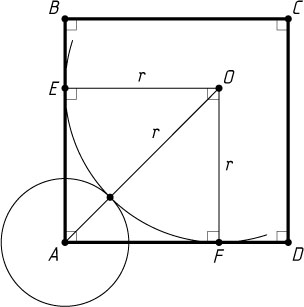
Пусть искомая окружность касается сторон AB
и AD
данного квадрата в точках E
и F
соответственно (рис. 3). Тогда AFOE
— квадрат со стороной r
, а AO
— его диагональ, поэтому r+2=r\sqrt{2}
, откуда r=2+2\sqrt{2}
. Тогда 2r=4+4\sqrt{2}\gt7
, значит, найденное решение не удовлетворяет условию задачи (найденный диаметр больше стороны данного квадрата).
Источник: Диагностические и тренировочные задачи ЕГЭ. — Задача C4, 2011


