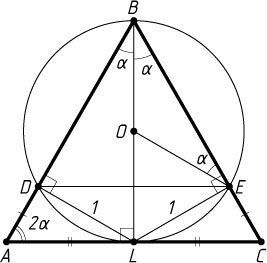
4955. На биссектрисе BL
треугольника ABC
как на диаметре построена окружность с центром в точке O
, пересекающая сторону AB
в точке D
, а сторону BC
— в точке E
, причём AD\cdot LC=EC\cdot AL
. Найдите площадь той части треугольника ABC
, которая лежит вне данной окружности, если известно, что \angle BAL=2\angle BEO
, DE=\sqrt{3}
.
Ответ. \frac{5\sqrt{3}}{6}-\frac{\pi}{3}
.
Решение. Точки D
и E
лежат на окружности с диаметром BL
, поэтому \angle BDL=\angle BEL=90^{\circ}
. Прямоугольные треугольники BDL
и BEL
равны по гипотенузе и острому углу, поэтому BD=BE
, а так как эти треугольники симметричны относительно прямой BL
(BL
— биссектриса треугольника ABC
), то DE\perp BL
.
Обозначим BD=BE=a
. По условию задачи и свойству биссектрисы треугольника
\frac{AD}{EC}=\frac{LC}{AL}=\frac{BC}{BA}=\frac{a+EC}{a+AD},
поэтому
a\cdot AD+AD^{2}=a\cdot EC+EC^{2}~\Rightarrow~a(EC-AD)=AD^{2}-EC^{2},
что возможно только, если EC=AD
. Тогда AB=BC
, т. е. треугольник ABC
— равнобедренный.
Обозначим \angle BEO=\alpha
. Тогда
\angle ABL=\angle CBL=\angle BEO=\alpha,~\angle BAL=2\alpha.
Биссектриса BL
равнобедренного треугольника ABC
является его высотой, поэтому треугольник ABL
— прямоугольный, значит, \alpha+2\alpha=90^{\circ}
. Следовательно, \alpha=30^{\circ}
. Тогда
\angle ABC=2\alpha=60^{\circ},~\angle DOE=2\angle ABC=120^{\circ},~EL=LD=1,
а так как основание DE
равнобедренного треугольника DOE
равно \sqrt{3}
, то R=OD=OE=1
, где R
— радиус окружности.
Пусть площадь сектора ODLE
равна S_{1}
, площадь треугольника BOD
(и BOE
) равна S_{2}
, а искомая площадь равна S
. Тогда
S_{1}=\frac{1}{3}\pi\cdot R^{2}=\frac{1}{3}\pi\cdot1=\frac{\pi}{3},
S_{2}=\frac{1}{2}OB\cdot OD\sin120^{\circ}=\frac{1}{2}R^{2}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4},
а площадь части треугольника ABC
, лежащей внутри окружности, равна
S_{1}+2S_{2}=\frac{\pi}{3}+\frac{\sqrt{3}}{2}.
Из прямоугольного треугольника ABL
находим, что AL=\frac{BL}{\sqrt{3}}=\frac{2}{\sqrt{3}}
, значит, AC=2AL=\frac{4}{\sqrt{3}}
, поэтому
S_{\triangle ABC}=\frac{1}{2}AC\cdot BL=\frac{1}{2}\cdot\frac{4}{\sqrt{3}}\cdot2=\frac{4}{\sqrt{3}}=\frac{4\sqrt{3}}{3}.
Следовательно, площадь части треугольника ABC
, которая лежит вне данной окружности, равна
S_{\triangle ABC}-(S_{1}+2S_{2})=\frac{4\sqrt{3}}{3}-\left(\frac{\pi}{3}+\frac{\sqrt{3}}{2}\right)=\frac{5\sqrt{3}}{6}-\frac{\pi}{3}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 2008, № 4, вариант 1
