4974. На сторонах AB
и BC
треугольника ABC
взяты точки E
и D
соответственно так, что \angle BAD=4\cdot\angle DAC
, \angle BCE=4\cdot\angle ECA
. Известно, что AB\cdot CE=BC\cdot AD
, AB=2
, радиус окружности, описанной около треугольника ABC
, равен \sqrt{4+2\sqrt{2}}
. Найдите площадь треугольника ABC
.
Ответ. \sqrt{2}
или \frac{\sqrt{3}+\sqrt{2}+1}{2}
.
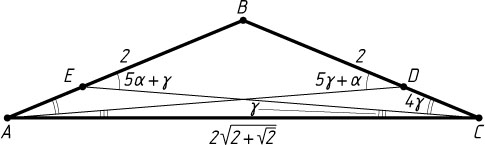
Решение. Положим \angle DAC=\alpha
, \angle BAD=4\alpha
, \angle ECA=\gamma
, \angle BCE=4\gamma
. По теореме о внешнем угле треугольника
\angle BEC=5\alpha+\gamma,~\angle ADB=5\gamma+\alpha.
Применяя теорему синусов к треугольникам BCE
и ABD
получим, что
\frac{CE}{\sin(5\gamma+5\alpha)}=\frac{BC}{\sin(5\alpha+\gamma)},~\frac{AB}{\sin(5\gamma+\alpha)}=\frac{AD}{\sin(5\gamma+5\alpha)}.
Перемножая почленно эти равенства и учитывая, что AB\cdot CE=BC\cdot AD
, получим, что \sin(5\gamma+\alpha)=\sin(5\alpha+\gamma)
. Следовательно, либо 5\gamma+\alpha=5\alpha+\gamma
, либо 5\gamma+\alpha+5\alpha+\gamma=180^{\circ}
.
В первом из этих случаев \alpha=\gamma
, во втором — \alpha+\gamma=30^{\circ}
.
Рассмотрим первый случай. Треугольник ABC
— равнобедренный, BC=AB=2
. Пусть R
— радиус описанной окружности треугольника ABC
, R=\sqrt{4+2\sqrt{2}}
. По теореме синусов
\sin\angle ACB=\sin5\gamma=\frac{AB}{2R}=\frac{2}{2\sqrt{4+2\sqrt{2}}}=\frac{1}{\sqrt{4+2\sqrt{2}}}=\frac{\sqrt{4-2\sqrt{2}}}{2\sqrt{2}}=\frac{\sqrt{2-\sqrt{2}}}{2},
а так как 5\gamma\lt90^{\circ}
как угол при основании равнобедренного треугольника, то \cos5\gamma\gt0
, поэтому
\cos5\gamma=\sqrt{1-\sin^{2}5\gamma}=\sqrt{1-\left(\frac{\sqrt{2-\sqrt{2}}}{2}\right)^{2}}=\frac{\sqrt{2+\sqrt{2}}}{2}.
Тогда
AC=2R\sin(180^{\circ}-10\gamma)=2R\sin10\gamma=4R\sin5\gamma\cos5\gamma=
=4\cdot\sqrt{4+2\sqrt{2}}\cdot\frac{\sqrt{2-\sqrt{2}}}{2}\cdot\frac{\sqrt{2+\sqrt{2}}}{2}=2\sqrt{2+\sqrt{2}}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AC\cdot BC\sin5\gamma=\frac{1}{2}\cdot2\sqrt{2+\sqrt{2}}\cdot2\cdot\frac{\sqrt{2-\sqrt{2}}}{2}=\sqrt{2}.
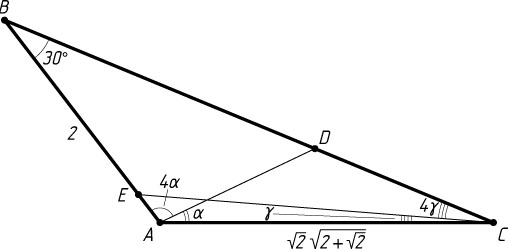
Рассмотрим второй случай. Пусть \alpha+\gamma=30^{\circ}
. Тогда
\angle ABC=180^{\circ}-5(\alpha+\gamma)=180^{\circ}-150^{\circ}=30^{\circ},
AC=2R\sin30^{\circ}=R=\sqrt{4+2\sqrt{2}}=\sqrt{2}\sqrt{2+\sqrt{2}},
\sin5\gamma=\frac{AB}{2R}=\frac{\sqrt{2-\sqrt{2}}}{2},
а так как AC=\sqrt{4+2\sqrt{2}}\gt2=AB
, то 5\gamma=\angle ACB\lt\angle ABC=30^{\circ}
, значит, \cos5\gamma\gt0
, поэтому
\cos5\gamma=\sqrt{1-\sin^{2}5\gamma}=\frac{\sqrt{2+\sqrt{2}}}{2}.
Тогда
\sin\angle BAC=\sin5\alpha=\sin(150^{\circ}-5\gamma)=\sin150^{\circ}\cos5\gamma-\cos150^{\circ}\sin5\gamma=
=\frac{1}{2}\cdot\frac{\sqrt{2+\sqrt{2}}}{2}+\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2-\sqrt{2}}}{2}=\frac{1}{4}\left(\sqrt{2+\sqrt{2}}+\sqrt{3}\sqrt{2-\sqrt{2}}\right).
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AC\cdot AB\sin5\alpha=\frac{1}{2}\cdot\sqrt{2}\sqrt{2+\sqrt{2}}\cdot2\cdot\frac{1}{4}\left(\sqrt{2+\sqrt{2}}+\sqrt{3}\sqrt{2-\sqrt{2}}\right)=
=\frac{\sqrt{2}}{4}(2+\sqrt{2}+\sqrt{3}\sqrt{2})=\frac{\sqrt{3}+\sqrt{2}+1}{2}.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 2008, отделение специалистов, июль, № 4, вариант 1

