4983. Диагональ AB
выпуклого четырёхугольника AKBC
делит его на два треугольника, один из которых равносторонний. Известно, что величина угла ACB
равна \frac{\pi}{2}+\arccos\frac{4}{\sqrt{43}}
, а расстояние от точки K
до центра окружности, описанной около треугольника ABC
, равно 6. Найдите радиус этой окружности.
Ответ. 2\sqrt{129}
.
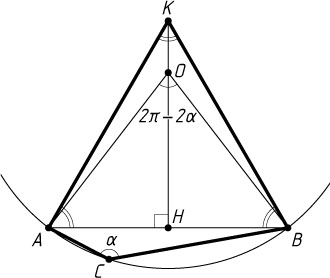
Решение. Пусть O
— центр окружности, описанной около треугольника ABC
, R
— радиус окружности, \alpha=\angle ACB=\frac{\pi}{2}+\arccos\frac{4}{\sqrt{43}}
.
По теореме синусов
AB=2R\sin\alpha=2R\sin\left(\frac{\pi}{2}+\arccos\frac{4}{\sqrt{43}}\right)=
=2R\cos\left(\arccos\frac{4}{\sqrt{43}}\right)=2R\cdot\frac{4}{\sqrt{43}}=\frac{8R}{\sqrt{43}}.
Докажем, что \angle AOB\gt\frac{\pi}{3}
. Это будет означать, что точка O
лежит внутри равностороннего треугольника AKB
, а значит, на его высоте KH
, а на не её продолжении. Действительно, AOB
— центральный угол, поэтому
\angle AOB=2\pi-\smile ACB=2\pi-2\angle ACB=2\pi-2\alpha=
=2\pi-\pi-2\arccos\frac{4}{\sqrt{43}}=\pi-2\arccos\frac{4}{\sqrt{43}},
\pi-2\arccos\frac{4}{\sqrt{43}}\gt\frac{\pi}{3}~\Leftrightarrow~\arccos\frac{4}{\sqrt{43}}\lt\frac{\pi}{3}~\Leftrightarrow~\frac{4}{\sqrt{43}}\gt\frac{1}{2}~\Leftrightarrow~8\gt\sqrt{43}.
Что и требовалось доказать.
Точка O
лежит на отрезке KH
, поэтому
OH=KH-KO=\frac{1}{2}AB\sqrt{3}-6=\frac{1}{2}\frac{8R}{\sqrt{43}}\cdot\sqrt{3}-6=\frac{4R\sqrt{3}}{\sqrt{43}}-6\gt0,
значит, R\gt\frac{1}{2}\sqrt{129}
.
По теореме Пифагора R^{2}=AH^{2}+OH^{2}
, или
R^{2}=\left(\frac{1}{2}\cdot\frac{8R}{\sqrt{43}}\right)^{2}+\left(\frac{4R\sqrt{3}}{\sqrt{43}}-6\right)^{2}~\Leftrightarrow~\frac{21}{43}R^{2}-\frac{48R\sqrt{3}}{\sqrt{43}}+36=0,
откуда находим, что R=2\sqrt{129}
или R=\frac{2}{7}\sqrt{129}
. Условию R\gt\frac{1}{2}\sqrt{129}
удовлетворяет только первый корень.
Источник: Вступительный экзамен на экономический факультет МГУ. — отделение менеджмента, 2007, № 6, вариант 1
