5004. Точки M
и N
расположены по одну сторону от прямой l
. С помощью циркуля и линейки постройте на прямой l
такую точку K
, для которой сумма MK+NK
была бы наименьшей.
Указание. Рассмотрите образ одной из данных точек при симметрии относительно прямой l
и примените неравенство треугольника.
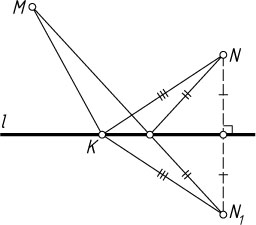
Решение. Пусть N_{1}
— точка, симметричная точке N
относительно прямой l
. Тогда для любой точки K
прямой l
MK+NK=MK+N_{1}K\geqslant MN_{1}.
Равенство достигается в случае, когда K
— точка пересечения прямых l
и MN_{1}
.
Примечание. Из этого утверждения следует, что касательная к эллипсу образует равные углы с фокальными радиусами, проведёнными в точку касания. (См. Д.Гильберт и С.Кон-Фоссен. Наглядная геометрия. Гл.1.)
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 13, с. 44
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 431, с. 25
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 77(а), с. 26
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 17.20, с. 58
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 17.20, с. 363
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — с. 90
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.40, с. 169
