5006. Точки M
и N
расположены по разные стороны от прямой l
и удалены от этой прямой на разные расстояния. С помощью циркуля и линейки постройте на прямой l
такую точку K
, чтобы разность отрезков MK
и NK
была наибольшей.
Указание. Рассмотрите образ одной из данных точек при симметрии относительно прямой l
и примените неравенство треугольника.
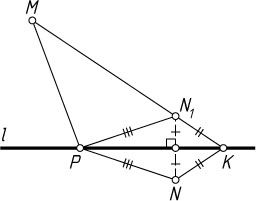
Решение. Пусть N_{1}
— точка, симметричная точке N
относительно прямой l
. Предположим, что прямая MN_{1}
пересекает прямую l
в точке K
. Докажем, что точка K
— искомая. Пусть P
— произвольная точка прямой l
, отличная от K
. Тогда
MP-NP=MP-N_{1}P\lt MN_{1}=MK-N_{1}K=MK-NK.
Примечание. Из этого утверждения следует, что касательная к гиперболе является биссектрисой угла между фокальными радиусами, проведёнными в точку касания. (См. Д.Гильберт и С.Кон-Фоссен. Наглядная геометрия. Гл.1.)
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 15, с. 44
Источник: Польские математические олимпиады. — 1954, задача 5
Источник: Страшевич С., Бровкин Е. Польские математические олимпиады. — М.: Мир, 1978. — № 35, с. 16
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 432, с. 25
