5058. На двух противоположных сторонах квадрата и на его диагоналях отмечено по точке. Квадрат стёрли, а отмеченные точки оставили. Восстановите квадрат.
Решение. Пусть точки K
и M
лежат на сторонах соответственно AB
и CD
квадрата ABCD
, а точки P
и Q
— на его диагоналях соответственно AC
и BD
, O
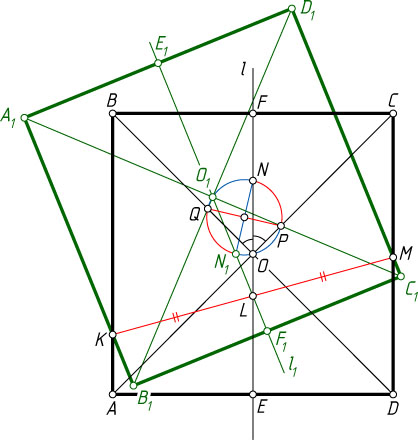
— центр квадрата. Рассмотрим случай, изображённый на рисунке.
Поскольку \angle POQ=90^{\circ}
, точка O
лежит на окружности с диаметром PQ
. Если отрезок, соединяющий середины E
и F
сторон соответственно AD
и BC
, пересекает эту окружность в точке N
, отличной от O
, то \angle QON=\angle EOD=45^{\circ}
. Значит, N
— середина полуокружности с диаметром PQ
. Кроме того, отрезок EF
проходит через середину L
отрезка KM
.
Отсюда вытекает следующее построение. На отрезке PQ
как на диаметре строим окружность. Проводим прямую l
через середину N
(или N_{1}
) одной из полуокружностей и середину L
отрезка KM
. Если эта прямая вторично пересекает полуокружность в точке O
, то O
— центр искомого квадрата. Стороны AB
и CD
искомого квадрата лежат на прямых, параллельных прямой l
. На прямой l
по разные стороны от точки O
откладываем отрезки OE
и OF
, равные половине расстояния между прямыми AB
и CD
, и через точки E
и F
проводим прямые, перпендикулярные прямой l
.
Если точка L
совпадает с N
(или N_{1}
) задача может иметь бесконечно много решений.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 1019, с. 125
