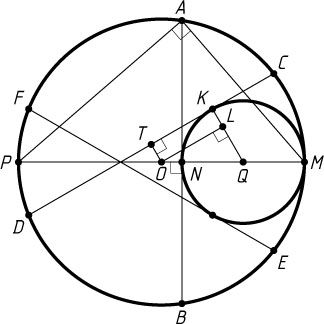
5148. Окружности радиусов 7 и 3 касаются внутренним образом. В большей окружности существуют ровно три различные хорды, имеющие одинаковую длину и касающиеся меньшей окружности. Найдите отрезки, на которые эти хорды делятся точками касания.
Ответ. 4\sqrt{3}
и 4\sqrt{3}
(одна из трёх хорд); 2\sqrt{3}
и 6\sqrt{3}
(две хорды).
Решение. Пусть O
и Q
— центры окружностей радиусов 7 и 3 соответственно, M
— точка касания окружностей, AB
— хорда большей окружности, перпендикулярная линии центров, CD
и EF
— две другие, равные ей хорды большей окружности, P
и N
соответственно — точки большей и меньшей окружностей, диаметрально противоположные точке M
. Поскольку окружности касаются, точки P
, O
, N
, Q
и M
лежат на одной прямой, причём точка O
— вне отрезка MN
, так как OM=7\gt6=MN
.
Отрезок AN
— высота прямоугольного треугольника AMP
, проведённая из вершины прямого угла, поэтому
AN=\sqrt{MN\cdot PN}=\sqrt{6\cdot8}=4\sqrt{3}.
Диаметр, перпендикулярный хорде, делит её пополам, поэтому BN=AN=4\sqrt{3}
.
Пусть хорда CD
большей окружности касается меньшей окружности в точке K
(CK\lt DK
), T
— середина CD
, L
— основание перпендикуляра, опущенного из точки O
на радиус QK
меньшей окружности. Равные хорды равноудалены от центра окружности, поэтому OT=ON=OM-MN=7-6=1
. В прямоугольном треугольнике OLQ
известно, что
OQ=OM-QM=7-3=4,~QL=QK-LK=QK-OT=3-1=2,
значит,
TK=OL=\sqrt{OQ^{2}-QL^{2}}=\sqrt{16-4}=2\sqrt{3}.
Следовательно,
CK=CT-TK=\frac{1}{2}CD-TK=4\sqrt{3}-2\sqrt{3}=2\sqrt{3},
DK=CD-CK=8\sqrt{3}-2\sqrt{3}=6\sqrt{3}.
Аналогично для хорды EF
.
Источник: Вступительный экзамен на филологический факультет МГУ. — 2006 июль, № 2, вариант 1
Источник: Вступительный экзамен на социологический факультет МГУ. — 2006 июль, № 2, вариант 1
