5192. В трапеции ABCD
, у которой AD\parallel BC
и AD:BC=2:1
, на боковых сторонах AB
и CD
выбраны соответственно точки E
и F
так, что AE\cdot DF=BE\cdot CF
. Отрезки AF
и DE
пересекаются в точке G
. Площадь треугольника ADG
в 6 раз меньше площади трапеции ABCD
. В каком отношении точка E
делит боковую сторону AB
?
Ответ. 2:1
или 1:2
.
Решение. Пусть продолжения боковых сторон AB
и BC
трапеции ABCD
пересекаются в точке O
. Тогда BC
— средняя линия треугольника AOD
(BC\parallel AD
и BC=\frac{1}{2}AD
). По условию задачи AE\cdot DF=BE\cdot CF
, поэтому \frac{AE}{BE}=\frac{CF}{DF}
. Обозначим AE=a
, BE=b
, DF=c
, CF=d
, \frac{a}{b}=\frac{d}{c}=x
. Тогда a=bx
, d=cx
.
Через вершину A
проведём прямую, параллельную CD
. Пусть эта прямая пересекается с прямой DG
в точке T
. Из подобия треугольников AET
и OED
следует, что
AT=\frac{AE}{OE}\cdot DO=\frac{bx}{b+b(1+x)}\cdot2c(1+x)=\frac{2cx(1+x)}{2+x},
а из подобия треугольников AGT
и FGD
—
\frac{AG}{GF}=\frac{AT}{DF}=\frac{\frac{2cx(1+x)}{2+x}}{c}=\frac{2x(1+x)}{2+x}.
Тогда
\frac{AG}{AF}=\frac{AG}{AG+GF}=\frac{2x(1+x)}{2x(1+x)+2+x}=\frac{2x(1+x)}{2x^{2}+3x+2}.
Пусть площадь трапеции равна S
, высота трапеции равна h
, а высота треугольника AFD
, опущенная на сторону AD
равна h_{1}
. Тогда
S=\frac{1}{2}(AD+BC)h=\frac{1}{2}\left(\frac{1}{2}AD+AD\right)h=\frac{3}{4}ADh,
S_{\triangle AFD}=\frac{1}{2}ADh_{1}=\frac{1}{2}AD\cdot\frac{1}{1+x}h=\frac{3}{4}ADh\cdot\frac{2}{3(1+x)}=\frac{2}{3(1+x)}\cdot S,
а так как
S_{\triangle ADG}=\frac{AG}{AF}\cdot S_{\triangle AFD}=\frac{2x(1+x)}{2x^{2}+3x+2}\cdot\frac{2}{3(1+x)}\cdot S=\frac{4x}{3(2x^{2}+3x+2)}\cdot S
и по условию S_{\triangle ADG}=\frac{1}{6}S
, то
\frac{4x}{3(2x^{2}+3x+2)}\cdot S=\frac{1}{6}S~\Leftrightarrow~\frac{8x}{2x^{2}+3x+2}=1~\Leftrightarrow~2x^{2}-5x+2=0.
Из этого уравнения находим, что x=2
или x=\frac{1}{2}
. Следовательно, \frac{AE}{BE}=2
или \frac{AE}{BE}=\frac{1}{2}
.
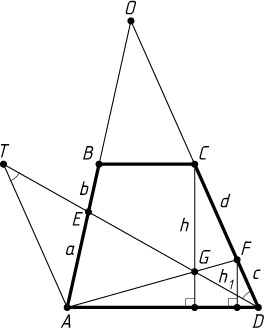
Источник: Математическая олимпиада МГУ «Покори Воробьёвы горы». — 2006, (очный тур, ВМиК), № 4
